
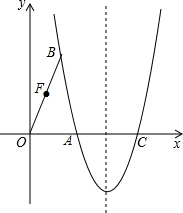
 ��ͼ����ƽ��ֱ������ϵ�У�������y=$\frac{8\sqrt{2}}{5}$x2+bx+c������A��$\frac{3}{2}$��0���͵�B��1��2$\sqrt{2}$������x�����һ������ΪC��
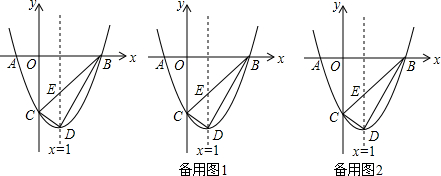
��ͼ����ƽ��ֱ������ϵ�У�������y=$\frac{8\sqrt{2}}{5}$x2+bx+c������A��$\frac{3}{2}$��0���͵�B��1��2$\sqrt{2}$������x�����һ������ΪC������ ��1����A��B���뺯������ʽ�������b��c��ֵ����ú�������ʽ��
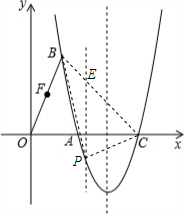
��2���������ô���ϵ�������ֱ��BC�Ľ���ʽ����P�ĺ�������t����P��y���ƽ���߽�BC�ڵ�E����E�����꼴����t��ʾ����EF�ij�������t��ʾ�����BCP��������ɱ�ʾ��t�ĺ��������ú��������ʼ�����⣻
��3����Rt��BNF�У��ɹ��ɶ������BF�ij���Ȼ��ֳɵ���Mλ�ڵ�B�Ҳ�ʱ�͵���Mλ�ڵ�B���ʱ��������������ۣ�����ֱ�������ε������Լ����������ε����ʼ�����⣮
���  �⣺��1����������ã�$\left\{\begin{array}{l}{\frac{8\sqrt{2}}{5}����\frac{3}{2}��^{2}+\frac{3}{2}b+c=0}\\{\frac{8\sqrt{2}}{5}+b+c=2\sqrt{2}}\end{array}\right.$��
�⣺��1����������ã�$\left\{\begin{array}{l}{\frac{8\sqrt{2}}{5}����\frac{3}{2}��^{2}+\frac{3}{2}b+c=0}\\{\frac{8\sqrt{2}}{5}+b+c=2\sqrt{2}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=-8\sqrt{2}}\\{c=\frac{42}{5}\sqrt{2}}\end{array}\right.$��
�����Ľ���ʽ�ǣ�$y=\frac{8}{5}\sqrt{2}{x^2}-8\sqrt{2}x+\frac{42}{5}\sqrt{2}$��
��2����$y=\frac{8}{5}\sqrt{2}{x^2}-8\sqrt{2}x+\frac{42}{5}\sqrt{2}$����y=0��
��ã�x=$\frac{3}{2}$��$\frac{7}{2}$��
A�������ǣ�$\frac{3}{2}$��0������C�������ǣ�$\frac{7}{2}$��0����
��BC�ĺ�������ʽ�ǣ�y=kx+d��
��$\left\{\begin{array}{l}{k+d=2\sqrt{2}}\\{\frac{7}{2}k+d=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{4\sqrt{2}}{5}}\\{d=\frac{14\sqrt{2}}{5}}\end{array}\right.$��
��ֱ��BC�Ľ���ʽ�ǣ�y=$-\frac{4\sqrt{2}}{5}$x+$\frac{14\sqrt{2}}{5}$��
��P�ĺ�������t����P��y���ƽ���߽�BC�ڵ�E����E�������ǣ�t��$\frac{-4\sqrt{2}}{5}$t+$\frac{14\sqrt{2}}{5}$����P�������ǣ�t��$\frac{8\sqrt{2}}{5}{t}^{2}-8\sqrt{2}t+\frac{42\sqrt{2}}{5}$����
��S��BCP=$\frac{1}{2}$[��$\frac{-4\sqrt{2}}{5}$t+$\frac{14\sqrt{2}}{5}$��-��$\frac{8\sqrt{2}}{5}{t}^{2}-8\sqrt{2}t+\frac{42\sqrt{2}}{5}$��]��$\frac{7}{2}$-1����
��S��BCP�����ֵ�ǣ�$\frac{137\sqrt{2}}{8}$��
��3����O��0��0����B��1��2$\sqrt{2}$����FΪOB���е㣬��F��$\frac{1}{2}$��$\sqrt{2}$����
����F��FN��ֱ��BD�ڵ�N����FN=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$��BN=1-$\frac{1}{2}$=$\frac{1}{2}$��
��Rt��BNF�У��ɹ��ɶ����ã�BF=$\sqrt{B{N}^{2}-F{N}^{2}}$=$\frac{3}{2}$��
�ߡ�BMF=$\frac{1}{3}$��MFO����MFO=��FBM+��BMF��
���FBM=2��BMF��
��I������Mλ�ڵ�B�Ҳ�ʱ��
��ֱ��BD�ϵ�B���ȡһ��G��ʹBG=BF=$\frac{3}{2}$������FG����GN=BG-BN=1��
��Rt��FNG�У��ɹ��ɶ����ã�FG=$\sqrt{G{N}^{2}+F{N}^{2}}$=$\sqrt{3}$��
��BG=BF�����BGF=��BFG��
�֡ߡ�FBM=��BGF+��BFG=2��BMF��
���BFG=��BMF���֡ߡ�MGF=��MGF��
���GFB�ס�GMF��
��$\frac{GM}{GF}$=$\frac{GF}{GB}$����$\frac{\frac{3}{2}+BM}{\sqrt{3}}=\frac{\sqrt{3}}{\frac{3}{2}}$��
��BM=$\frac{1}{2}$��
��II������Mλ�ڵ�B���ʱ��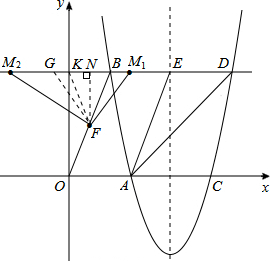
��BD��y�ύ�ڵ�K������FK����FKΪRt��KOBб���ϵ����ߣ�
��KF=$\frac{1}{2}$OB=FB=$\frac{3}{2}$��
���FKB=��FBM=2��BMF��
�֡ߡ�FKB=��BMF+��MFK��
���BMF=��MFK��
��MK=KF=$\frac{3}{2}$��
��BM=MK+BK=$\frac{3}{2}$+1=$\frac{5}{2}$��
�����������߶�BM�ij�Ϊ$\frac{1}{2}$��$\frac{5}{2}$��
���� ���⿼���˴���ϵ������ú�������ʽ���Լ����ö��κ�������������ֵ����ȷ���������ǽ������Ĺؼ���


 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
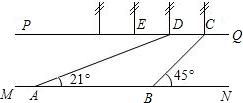 ��ü���Ƕ�ü��һ���羰�㣮��ͼ���ӵ�����PQƽ����MN���Ӱ�PQ����һ�ż��Ϊ50�IJʵ���C��D��E������С���ںӰ�MN��A����á�DAN=21�㣬Ȼ���غӰ�����175����B������á�CBN=45�㣬�������ӵĿ��ȣ��ο����ݣ�sin21���$\frac{9}{25}$��tan21���$\frac{3}{8}$����
��ü���Ƕ�ü��һ���羰�㣮��ͼ���ӵ�����PQƽ����MN���Ӱ�PQ����һ�ż��Ϊ50�IJʵ���C��D��E������С���ںӰ�MN��A����á�DAN=21�㣬Ȼ���غӰ�����175����B������á�CBN=45�㣬�������ӵĿ��ȣ��ο����ݣ�sin21���$\frac{9}{25}$��tan21���$\frac{3}{8}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
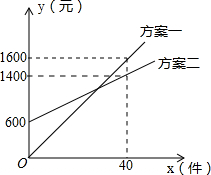 ij���۹�˾����һ�ֲ�Ʒ����x���֣���������Ʒ��������y��Ԫ���Ǹ�������Ա���±��꣮��˾��������Ա���±�������ַ�����ͼ��ʾ������Ա������ѡһ���빫˾ǩ����ͬ����ͼ����������⣺
ij���۹�˾����һ�ֲ�Ʒ����x���֣���������Ʒ��������y��Ԫ���Ǹ�������Ա���±��꣮��˾��������Ա���±�������ַ�����ͼ��ʾ������Ա������ѡһ���빫˾ǩ����ͬ����ͼ����������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
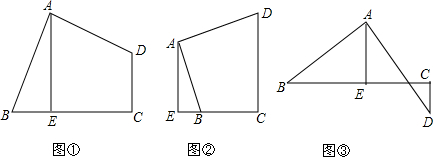
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
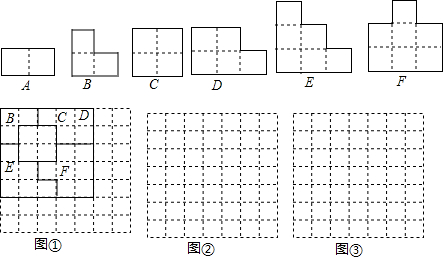
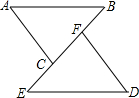 ��ͼ����ABC���DEF��ȫ�������Σ�����ABC�ա�DEF����ôͼ����ȵ��߶��У�������
��ͼ����ABC���DEF��ȫ�������Σ�����ABC�ա�DEF����ôͼ����ȵ��߶��У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com