
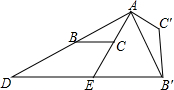
 如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.
如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$. 分析 延长AC′,交BD′的延长线于F,根据已知求得∠AEB′=60°,∠F=30°,进而求得△B′FC′是直角三角形,设C′F=x,则B′F=$\frac{\sqrt{3}}{2}$x,在RT△AEF中,解直角三角形求得cos∠F=$\frac{AF}{EF}$=$\frac{\sqrt{3}}{2}$,求得x的值,即可求得B′C′=2,得出AC′=B′C′,求得∠B′AC′=30°,得出∠EAB′=60°,根据等角对等边,即可求得AB=2$\sqrt{3}$.
解答 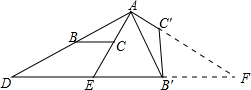 解:延长AC′,交BD′的延长线于F,
解:延长AC′,交BD′的延长线于F,
∵∠AED=120°,
∴∠AEB′=60°,
∵∠EAF=90°,
∴∠F=30°,
∵BC∥DE,
∴∠ACB=∠AED=120°,
∴∠AC′B′=120°
∴∠B′C′F=60°,
∴∠C′B′F=90°,
∴B′C′=$\frac{1}{2}$C′F,B′F=$\frac{\sqrt{3}}{2}$C′F,
设C′F=x,则B′F=$\frac{\sqrt{3}}{2}$x,
∵AC=AC′=2,EB′=2$\sqrt{3}$,
∴AF=2+x,EF=2$\sqrt{3}$+$\frac{\sqrt{3}}{2}$x,
∴cos∠F=$\frac{AF}{EF}$=$\frac{\sqrt{3}}{2}$,
即$\frac{2+x}{2\sqrt{3}+\frac{\sqrt{3}}{2}x}$=$\frac{\sqrt{3}}{2}$,
解得x=4,
∴B′C′=$\frac{1}{2}$x=2,
∴AC′=B′C′,
∵∠B′C′F=60°,
∴∠B′AC′=30°,
∴∠EAB′=60°,
∴∠EAB=∠AEB′
∴AB′=BE=2$\sqrt{3}$,
∴AB=2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
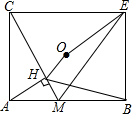 如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )
如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
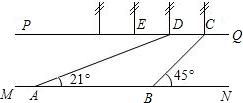 峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).
峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△AED中,∠E=90°,AE=6,cosA=$\frac{3}{5}$,求AD、ED、sin∠D、cos∠D、tan∠D的值.
如图,在Rt△AED中,∠E=90°,AE=6,cosA=$\frac{3}{5}$,求AD、ED、sin∠D、cos∠D、tan∠D的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
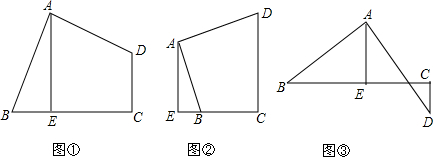
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
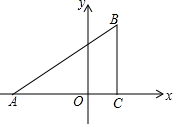 已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=3.
已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解八年级学生的课外阅读情况,学习随机调查了该年级25名学生,得到了他们上周双休日课外阅读时间(记为t,单位:时)的一组数据样本,其扇形统计图如图所示.
为了了解八年级学生的课外阅读情况,学习随机调查了该年级25名学生,得到了他们上周双休日课外阅读时间(记为t,单位:时)的一组数据样本,其扇形统计图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com