
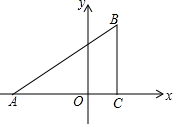
 已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=3.
已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=3.分析 (1)先根据∠ACB=90°,C(1,0),BC=3求出B点坐标,利用待定系数法求出直线AB的解析式即可;
(2)运用相似三角形的性质就可求出点D的坐标;
(3)由于△APQ与△ADB已有一组公共角相等,只需分△APQ∽△ABD和△APQ∽△ADB两种情况讨论,然后运用相似三角形的性质建立关于m的方程,就可解决问题
解答 解:(1)∵∠ACB=90°,C(1,0),BC=3,
∴B(1,3).
设过点AB的解析式为y=kx+b(k≠0),
∵A(-3,0),B(1,3),
∴$\left\{\begin{array}{l}0=-3k+b\\ 3=k+b\end{array}\right.$,解得$\left\{\begin{array}{l}k=\frac{3}{4}\\ b=\frac{9}{4}\end{array}\right.$,
∴直线AB的解析式为:y=$\frac{3}{4}$x+$\frac{9}{4}$;
(2)若△ADB与△ABC相似(不包括全等),则有∠ABD=90°,如图1,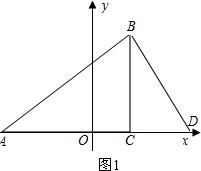
此时$\frac{AB}{AC}$=$\frac{AD}{AB}$,即AB2=AC•AD.
∵∠ACB=90°,AC=4,BC=3,
∴AB=5,
∴25=4AD,
∴AD=$\frac{25}{4}$,
∴OD=AD-AO=$\frac{25}{4}$-3=$\frac{13}{4}$,
∴点D的坐标为($\frac{13}{4}$,0).
(3)∵AP=DQ=m,
∴AQ=AD-QD=$\frac{25}{4}$-m.
①若△APQ∽△ABD,如图2,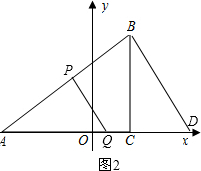
则有$\frac{AP}{AB}$=$\frac{AQ}{AD}$,
∴AP•AD=AB•AQ,
∴$\frac{25}{4}$m=5($\frac{25}{4}$-m),
解得m=$\frac{5}{9}$.
②若△APQ∽△ADB,如图3,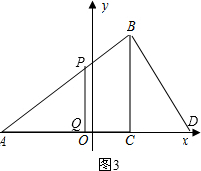
则有$\frac{AP}{AD}$=$\frac{AQ}{AB}$,
∴AP•AB=AD•AQ,
∴5m=$\frac{25}{4}$($\frac{25}{4}$-m),
解得:m=$\frac{125}{36}$.
综上所述:符合要求的m的值为$\frac{25}{9}$或$\frac{125}{36}$.
点评 本题考查的是一次函数综合题,涉及到相似三角形的判定与性质、勾股定理等知识,考查了分类讨论的数学思想,属于中档题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
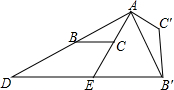 如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.
如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| B. | 购买一张福利彩票,中奖 | |
| C. | -2的绝对值小于0 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
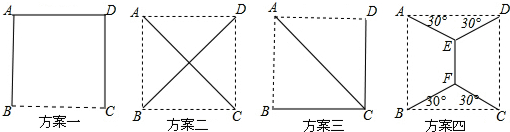
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
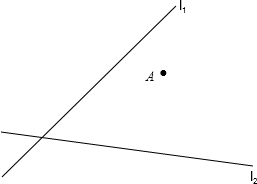 如图,点A表示城镇,直线l1,l2表示两条相交的公路,电信部门要修建一座信号发射塔P,按照设计要求,发射塔到两条公路l1,l2的距离必须相等,且使发射塔P到A的距离最短,请用尺规作图确定发射塔P的位置(保留作图痕迹,不要求写出画法)
如图,点A表示城镇,直线l1,l2表示两条相交的公路,电信部门要修建一座信号发射塔P,按照设计要求,发射塔到两条公路l1,l2的距离必须相等,且使发射塔P到A的距离最短,请用尺规作图确定发射塔P的位置(保留作图痕迹,不要求写出画法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com