
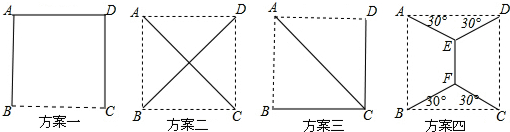
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
分析 设正方形的边长为a,计算出各种情况时正方形的面积,然后进行比较从而解得.
解答 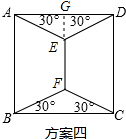 解:设正方形边长为a,则方案①需用线3a,方案②需用线2$\sqrt{2}$a,方案③需用线2a+$\sqrt{2}$a,
解:设正方形边长为a,则方案①需用线3a,方案②需用线2$\sqrt{2}$a,方案③需用线2a+$\sqrt{2}$a,
如图所示:
∵AD=a,
∴AG=$\frac{a}{2}$,AE=$\frac{\sqrt{3}}{3}$a,GE=$\frac{\sqrt{3}}{6}$a,
∴EF=a-2GE=a-$\frac{\sqrt{3}}{3}$a,
∴方案④需用线$\frac{\sqrt{3}}{3}$a×4+(a-$\frac{\sqrt{3}}{6}$a×2)=($\sqrt{3}$+1)a.
∴方案④最省钱.
故选D.
点评 本题考查的是作图-应用与设计作图,涉及到正方形的性质,设其正方形边长,分别计算出各自的面积,进行比较而得.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
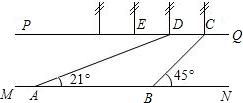 峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).
峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
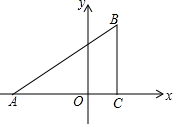 已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=3.
已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
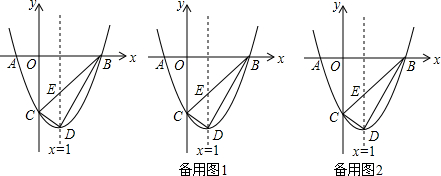
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com