
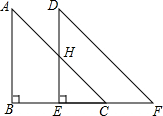
 如图,将直角△ABC沿BC边平移得到直角△DEF,AB=6cm,BE=3cm,DH=3cm,求四边形CHDF的面积为多少cm2?
如图,将直角△ABC沿BC边平移得到直角△DEF,AB=6cm,BE=3cm,DH=3cm,求四边形CHDF的面积为多少cm2? 分析 根据平移的性质得△ABC≌△DEF,DE=AB=6,则S△ABC=S△DEF,HE=DE-DH=3,所以S四边形CHDF=S梯形ABEH,然后根据梯形的面积公式计算即可.
解答 解:∵直角△ABC沿BC边平移得到直角△DEF,
∴△ABC≌△DEF,DE=AB=6,
∴S△ABC=S△DEF,HE=DE-DH=6-3=3,
∴S四边形CHDF=S梯形ABEH=$\frac{1}{2}$×(3+6)×3=$\frac{27}{2}$(cm2).
答:四边形CHDF的面积为$\frac{27}{2}$cm2.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
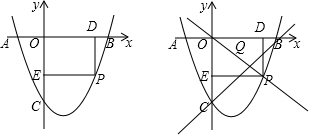
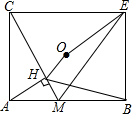 如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )
如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
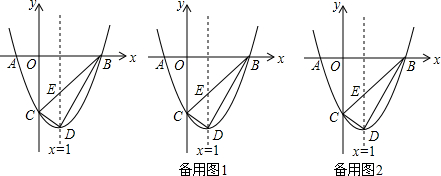
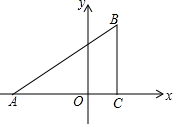 已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=3.
已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解八年级学生的课外阅读情况,学习随机调查了该年级25名学生,得到了他们上周双休日课外阅读时间(记为t,单位:时)的一组数据样本,其扇形统计图如图所示.
为了了解八年级学生的课外阅读情况,学习随机调查了该年级25名学生,得到了他们上周双休日课外阅读时间(记为t,单位:时)的一组数据样本,其扇形统计图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com