
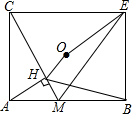
 如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )
如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①首先根据相似三角形判定的方法,判断出△ACM∽△HAM,即可判断出$\frac{AM}{MH}=\frac{MC}{AM}$,所以AM2=MH•MC;然后根据M为AB的中点,可得AM=BM,据此推得BM2=MH•MC即可.
②首先根据全等三角形判定的方法,判断出△ACM≌△BEM,即可推得MC=ME,所以△MCE为等腰三角形;然后根据无法判断CM、CE的关系,推得△MCE为等边三角形这个结论不正确.
③首先连接BC,判断出BH=OE=$\frac{1}{2}$BC;然后根据BM2=MH•MC,判断出△BMH∽△CMB,即可判断出MB=2MH,据此推得∠HAM=30°,∠ACH=30°,AH=$\frac{\sqrt{3}}{2}AM$,AC=$\frac{\sqrt{3}}{2}AB$,所以$\frac{AC}{AB}$=$\frac{{\sqrt{3}}}{2}$;最后根据OE=OC,可得∠CEO=∠ECO,据此求出tan∠CEO的值是多少即可.
④首先延长HO交CE于点D,假设OH∥EM,则推得CH=DH;然后根据已知条件无法判断出CH=DH,所以OH∥EM不成立,据此判断即可.
解答 解:∵AH⊥CM,
∴∠AMH+∠HAM=90°,
又∵∠AMH+∠ACM=90°,
∴∠ACM=∠HAM,
在△ACM和△HAM中,
$\left\{\begin{array}{l}{∠ACM=∠HAM}\\{∠CAM=∠AHM}\end{array}\right.$
∴△ACM∽△HAM,
∴$\frac{AM}{MH}=\frac{MC}{AM}$,
∴AM2=MH•MC,
又∵M为AB的中点,
∴AM=BM,
∴BM2=MH•MC,
∴结论①正确.
在△ACM和△BEM中,
$\left\{\begin{array}{l}{AM=BM}\\{∠CAM=∠EBM}\\{AC=BE}\end{array}\right.$
∴△ACM≌△BEM,
∴MC=ME,
∴△MCE为等腰三角形,
∵无法判断CM、CE的关系,
∴不能确定△MCE为等边三角形,
∴结论②不正确.
如图1,连接BC,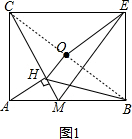 ,
,
∵点0为矩形ABEC的中心,
∴BC所在的直线经过点O,
∵点O是BC边的中点,
∴OE=$\frac{1}{2}BC$,
又∵BH=OE,
∴BH=OE=$\frac{1}{2}$BC,
∵BM2=MH•MC,
∴$\frac{BM}{MC}=\frac{MH}{BM}$,
∴△BMH∽△CMB,
∴$\frac{MH}{MB}=\frac{BH}{CB}=\frac{1}{2}$,
∴MB=2MH,
又∵AM=MB,
∴AM=2MH,
∴∠HAM=30°,
∴∠ACH=30°,AH=$\frac{\sqrt{3}}{2}AM$,
∴AC=2AH=2×$\frac{\sqrt{3}}{2}AM$=$\sqrt{3}$AM=$\sqrt{3}×\frac{1}{2}AB$=$\frac{\sqrt{3}}{2}AB$,
∴$\frac{AC}{AB}$=$\frac{{\sqrt{3}}}{2}$,
∵OE=OC,
∴∠CEO=∠ECO,
∴tan∠CEO=tan∠ECO=$\frac{BE}{CE}$=$\frac{AC}{AB}$=$\frac{{\sqrt{3}}}{2}$,
∴若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$,
∴结论③正确.
如图2,延长HO交CE于点D,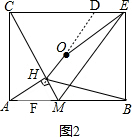 ,
,
假设OH∥EM,
则$\frac{DH}{EM}=\frac{CH}{CM}$,
∵CM=EM,
∴CH=DH,
∵无法判断CH=DH,
∴OH∥EM不成立,
∴结论④不正确.
综上,可得
正确的结论的个数是2个:①③.
故选:B.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.
(3)此题还考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①判定定理1:SSS--三条边分别对应相等的两个三角形全等.②判定定理2:SAS--两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA--两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS--两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL--斜边与直角边对应相等的两个直角三角形全等.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,内切圆O与各边分别切于点D、E、F
如图,在△ABC中,∠C=90°,内切圆O与各边分别切于点D、E、F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
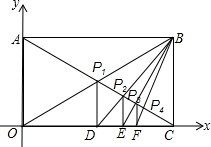 平面直角坐标系中,矩形OABC的顶点A,C分别在坐标轴上,顶点B在第一象限内,如图所示,且OA=a,OC=b.请根据下列操作,完成后面的问题.
平面直角坐标系中,矩形OABC的顶点A,C分别在坐标轴上,顶点B在第一象限内,如图所示,且OA=a,OC=b.请根据下列操作,完成后面的问题.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
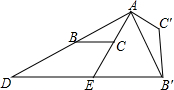 如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.
如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com