
 如图,在△ABC中,∠C=90°,内切圆O与各边分别切于点D、E、F
如图,在△ABC中,∠C=90°,内切圆O与各边分别切于点D、E、F分析 (1)先根据切线的性质得出CE=CF,∠OEF=∠OFC=90°,再由∠C=90°即可得出结论;
(2)连接OA,OB,OC,OD,先根据勾股定理求出AC的长,再设⊙O的半径为r,利用三角形的面积公式即可得出结论.
解答 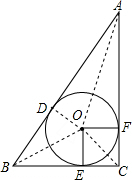 (1)证明:∵BC、AC是⊙O的切线,
(1)证明:∵BC、AC是⊙O的切线,
∴CE=CF,∠OEF=∠OFC=90°.
∵∠C=90°,
∴四边形OECF为正方形;
(2)连接OA,OB,OC,OD,
∵在△ABC中,∠C=90°,AB=6,BC=4,
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$.
设⊙O的半径为r,则S△ABC=S△AOC+S△BOC+S△AOB=$\frac{1}{2}$AC•BC=$\frac{1}{2}$(AC+BC+AB)•r,
即8$\sqrt{5}$=(2$\sqrt{5}$+6+4)r,解得r=$\sqrt{5}$-1.
点评 本题考查的是三角形的内切圆与内心,熟知三角形的内心就是三角形三个内角角平分线的交点是解答此题的关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
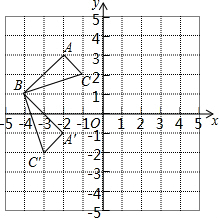 在平面直角坐标系中,△ABC的位置如图所示,网格中小正方形的边长为1,请回答下列问题:
在平面直角坐标系中,△ABC的位置如图所示,网格中小正方形的边长为1,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
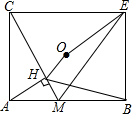 如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )
如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com