

分析 首先判断出这些四边形的其中两条边的长度都是1;然后分别求出1个梯形的周长、第2个这样的梯形镶嵌而成的四边形的周长、第3个这样的梯形镶嵌而成的四边形的周长各是多少,总结出规律,判断出第n个这样的梯形镶嵌而成的四边形的周长y等于多少即可.
解答 解:1个梯形的周长是:
(1+2)+(1+1)=3+2=3×1+2,
第2个这样的梯形镶嵌而成的四边形的周长是:
(3+3)+(1+1)=6+2=3×2+2,
第3个这样的梯形镶嵌而成的四边形的周长是:
(4+5)+(1+1)=9+2=3×3+2,
…,
∴第n个这样的梯形镶嵌而成的四边形的周长是:y=3n+2.
故答案为:3n+2.
点评 (1)此题主要考查了图形的变化类问题,要熟练掌握,解答此类问题的关键是首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.
(2)解答此题的关键是熟练掌握四边形的周长的含义和求法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,内切圆O与各边分别切于点D、E、F
如图,在△ABC中,∠C=90°,内切圆O与各边分别切于点D、E、F查看答案和解析>>
科目:初中数学 来源: 题型:填空题
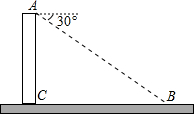 如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为10$\sqrt{3}$m(结果保留根号).
如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为10$\sqrt{3}$m(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com