
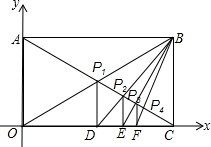
 平面直角坐标系中,矩形OABC的顶点A,C分别在坐标轴上,顶点B在第一象限内,如图所示,且OA=a,OC=b.请根据下列操作,完成后面的问题.
平面直角坐标系中,矩形OABC的顶点A,C分别在坐标轴上,顶点B在第一象限内,如图所示,且OA=a,OC=b.请根据下列操作,完成后面的问题.分析 【操作】(1)由矩形的性质得出∠AOC=90°,OA=BC,OA∥BC,P1A=P1C=$\frac{1}{2}$AC,P1O=P1B=$\frac{1}{2}$OB,证出P1D是△AOC的中位线,得出P1D=$\frac{1}{2}$OA=$\frac{1}{2}$a即可;
(2)由平行线得出△DP1P2∽△BCP2,得出对应边成比例$\frac{{P}_{1}{P}_{2}}{C{P}_{2}}=\frac{D{P}_{1}}{BC}$=$\frac{1}{2}$,求出P2E即可;
(3)同(2),即可得出结果;
【问题】(1)由【操作】(1)(2)(3)得出规律,即可得出结果;
(2)由以上得出规律,即可得出结果.
解答 解:【操作】(1)∵四边形OABC是矩形,
∴∠AOC=90°,OA=BC=a,OA∥BC,P1A=P1C=$\frac{1}{2}$AC,P1O=P1B=$\frac{1}{2}$OB,
∵P1D⊥x轴,
∴P1D∥AO,
∴P1D是△AOC的中位线,
∴P1D=$\frac{1}{2}$OA=$\frac{1}{2}$a,
∴点P1的纵坐标为$\frac{1}{2}$a;
故答案为:$\frac{1}{2}$a;
(2)∵P1D∥OA,OA∥BC,
∴P1D∥BC,
∴△DP1P2∽△BCP2,
∴$\frac{{P}_{1}{P}_{2}}{C{P}_{2}}=\frac{D{P}_{1}}{BC}$=$\frac{1}{2}$,
∵P1D⊥x轴,P2E⊥x轴,
∴P2E∥P1D,
∴$\frac{{P}_{2}E}{{P}_{1}D}=\frac{C{P}_{2}}{C{P}_{1}}$=$\frac{2}{3}$,
∴P2E=$\frac{2}{3}$×$\frac{1}{2}$a=$\frac{1}{3}$a,
∴点P2的纵坐标为$\frac{1}{3}$a;
故答案为:$\frac{1}{3}$a;
(3)同(2)可得:点P3的纵坐标为$\frac{1}{4}$a;
故答案为:$\frac{1}{4}$a;
【问题】(1)由:【操作】(1)(2)(3)得出规律,点P4的纵坐标为$\frac{1}{5}$a;
(2)由以上得出规律:点Pn(n为正整数)的纵坐标是$\frac{a}{n+1}$;
故答案为:$\frac{a}{n+1}$.
点评 本题是四边形综合题目,考查了矩形的性质、三角形中位线定理、相似三角形的判定与性质、平行线的判定等知识;本题有一定难度,综合性强,需要运用三角形中位线定理和三角形相似才能得出结果,得出规律.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
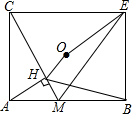 如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )
如图,点0为矩形ABEC的中心;M为AB的中点,AH⊥CM于H,连OE,EM,BH,下列结论:①BM2=MH•MC;②△MCE为等边△;③若BH=OE,则tan∠CEO=$\frac{{\sqrt{3}}}{2}$;④OH∥EM,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
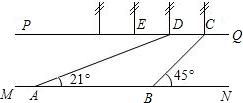 峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).
峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com