
 如图,在Rt△AED中,∠E=90°,AE=6,cosA=$\frac{3}{5}$,求AD、ED、sin∠D、cos∠D、tan∠D的值.
如图,在Rt△AED中,∠E=90°,AE=6,cosA=$\frac{3}{5}$,求AD、ED、sin∠D、cos∠D、tan∠D的值. 分析 首先利用锐角三角函数关系得出AD的长,再利用勾股定理得出DE的长,进而分别得出sin∠D、cos∠D、tan∠D的值.
解答 解:∵∠E=90°,AE=6,cosA=$\frac{3}{5}$,
∴cosA=$\frac{AE}{AD}$=$\frac{3}{5}$=$\frac{6}{AD}$,
解得:AD=10,
则DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=8,
故sin∠D=$\frac{AE}{AD}$=$\frac{6}{10}$=$\frac{3}{5}$、cos∠D=$\frac{DE}{AD}$=$\frac{8}{10}$=$\frac{4}{5}$、tan∠D=$\frac{AE}{DE}$=$\frac{6}{8}$=$\frac{3}{4}$.
点评 此题主要考查了解直角三角形,正确记忆各锐角三角函数关系是解题关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
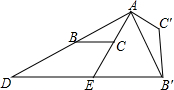 如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.
如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| B. | 购买一张福利彩票,中奖 | |
| C. | -2的绝对值小于0 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com