
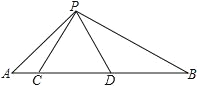
【题目】如图,点 C、D 在线段 AB 上,△PCD 是等边三角形,∠APB=120°
(1) 求证:△ACP∽△PDB
(2) 若 PC=3,AC=1,求 BD 的长
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字2,3,4,x,甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验,实验数据如下表:
摸球总次数 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为6”出现的频数 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为6”出现的频数 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为6”的频率将稳定在它的概率附近,估计出现“和为6”的概率是 .
(2)当x=5时,请用列表法或树状图法计算“和为6”的概率
(3)判断x=5是否符合(1)的结论,若符合,请说明理由,若不符合,请你写出一个符合(1)的x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
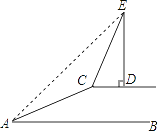
【题目】如图,某河大堤上有一颗大树ED,小明在A处测得树顶E的仰角为45°,然后沿坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,已知ED⊥CD,并且CD与水平地面AB平行,求大树ED的高度.(精确到1米)
(参考数据:sin76°≈0.97,cos76°=0.24,tan76°≈4.01, ![]() =2.236)
=2.236)
查看答案和解析>>
科目:初中数学 来源: 题型:
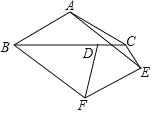
【题目】如图,在等腰△ABC 中,∠BAC=120°,AB=AC=2![]() ,点 D 在边 BC 上,CD=
,点 D 在边 BC 上,CD=![]() ,将线段 CD 绕点 C 逆时针旋转α°(其中 0<α≤360)到 CE,连接AE,以 AB,AE 为边作 ABFE,连接 DF,则 DF 的最大值为( )
,将线段 CD 绕点 C 逆时针旋转α°(其中 0<α≤360)到 CE,连接AE,以 AB,AE 为边作 ABFE,连接 DF,则 DF 的最大值为( )
A. ![]() +
+![]() B.
B. ![]() +
+![]() C. 2
C. 2![]() +
+![]() D.
D. ![]() +2
+2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
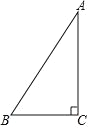
【题目】如图,△ABC 中,∠C=90°,将△ABC 绕点 C 顺时针旋转 90°,得到△DEC(其中点 D、E 分别是 A、B 两点旋转后的对应点).
(1)请画出旋转后的△DEC;
(2)试判断 DE 与 AB 的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
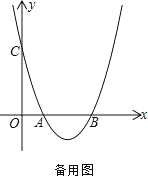
【题目】抛物线 y=ax2+bx+3 经过点(2,-1),与 x 轴交于 A(1,0)、B 两点,与 y轴交于点 C
(1) 求抛物线解析式
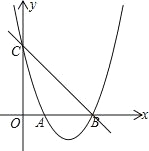
(2) 如图,点 E 是直线 BC 下方抛物线上的一动点.当△BEC 面积最大时,请求出点 E 的坐标
(3) 点 P 是第四象限内抛物线上的一动点,PA 交 y 轴于 D,BP 交 y 轴于 E,过 P 作 PN⊥y 轴于N,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
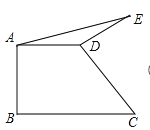
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至ED,连接AE、DE,△ADE的面积为3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
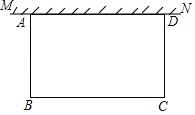
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com