
【题目】如图,某河大堤上有一颗大树ED,小明在A处测得树顶E的仰角为45°,然后沿坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,已知ED⊥CD,并且CD与水平地面AB平行,求大树ED的高度.(精确到1米)
(参考数据:sin76°≈0.97,cos76°=0.24,tan76°≈4.01, ![]() =2.236)
=2.236)

【答案】12米
【解析】
解:过点D作DF⊥AB于点F,过点C作CG⊥AB于点G,
∵ED⊥CD,CD∥AB,
∴D、E、F三点共线,
∴四边形CDFG是矩形,
∴CD=GF,DF=CG.
在Rt△ACG中,
∵坡度为1:2,
∴CG:AG=1:2,
∴AG:AC=2: ![]() .
.
∵AC=20米,
∴AG=8![]() 米,CG=4
米,CG=4![]() 米.
米.
在Rt△CDE中,∠ECD=76°,设CD=x米,则ED=CDtan76°≈4.01x(米).
在Rt△EAF中,
∵∠EAF=45°,
∴EF=AF,即ED+DF=AG+GF,
∴4.01x+4 ![]() =8
=8 ![]() +x,
+x,
∴x=2.99,
∴ED=4.01×2.99=12(米).
答:大树ED的高约为12米.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
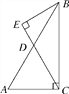
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点 C的对应点 C′恰好落在CB的延长线上,边AB交边 C′D′于点E.
(1)求证:BC=BC′;
(2)若 AB=2,BC=1,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
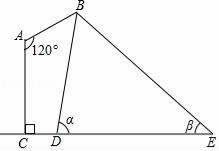
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到________元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 C、D 在线段 AB 上,△PCD 是等边三角形,∠APB=120°
(1) 求证:△ACP∽△PDB
(2) 若 PC=3,AC=1,求 BD 的长

查看答案和解析>>
科目:初中数学 来源: 题型:
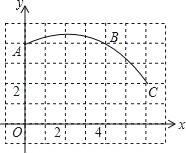
【题目】如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,完成下列问题:
(1)在图中标出圆心D,则圆心D点的坐标为 ;
(2)连接AD、CD,则∠ADC的度数为 ;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com