
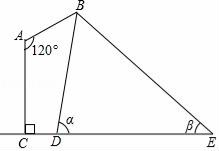
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
【答案】灯杆AB的长度为2米.
【解析】过点B作BF⊥CE,交CE于点F,过点A作AG⊥AF,交BF于点G,则FG=AC=11.设BF=3x知EF=4x、DF=![]() ,由DE=18求得x=4,据此知BG=BF-GF=1,再求得∠BAG=∠BAC-∠CAG=30°可得AB=2BG=2.
,由DE=18求得x=4,据此知BG=BF-GF=1,再求得∠BAG=∠BAC-∠CAG=30°可得AB=2BG=2.
过点B作BF⊥CE,交CE于点F,过点A作AG⊥AF,交BF于点G,则FG=AC=11.

由题意得∠BDE=α,tan∠β=![]() .
.
设BF=3x,则EF=4x
在Rt△BDF中,∵tan∠BDF=![]() ,
,
∴DF=![]() ,
,
∵DE=18,
∴![]() x+4x=18.
x+4x=18.
∴x=4.
∴BF=12,
∴BG=BF-GF=12-11=1,
∵∠BAC=120°,
∴∠BAG=∠BAC-∠CAG=120°-90°=30°.
∴AB=2BG=2,
答:灯杆AB的长度为2米.


科目:初中数学 来源: 题型:
【题目】“湖田十月清霜堕,晚稻初香蟹如虎”,又到了食蟹的好季节啦!某经销商去水产批发市场采购牟山湖大闸蟹,他看中了![]() 两家的某种品质相近的大闸蟹.零售价都为80元/千克,批发价各不相同.
两家的某种品质相近的大闸蟹.零售价都为80元/千克,批发价各不相同.
![]() 家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0-50部分 | 50以上-150的部分 | 150以上-250的部分 | 250以上的部分 |
价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发70千克牟山湖大闸蟹,则他在![]() 两家批发分别需要多少元;
两家批发分别需要多少元;
(2)如果他批发![]() 千克牟山湖大闸蟹(
千克牟山湖大闸蟹(![]() ),请你分别用含字母
),请你分别用含字母![]() 的式子表示他在
的式子表示他在![]() 两家批发所需的费用;
两家批发所需的费用;
(3)现在他要批发180千克山湖大闸蟹,你能帮助他选择哪家批发更便宜吗.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
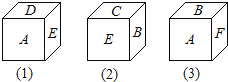
【题目】一个小立方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图.
(1)A对面的字母是_____,B对面的字母是_____,E对面的字母是_____.(请直接填写答案)
(2)若A=2x﹣1,B=﹣3x+9,C=﹣5,D=1,E=4x+5,F=9,且字母A与它对面的字母表示的数互为相反数,求B、E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
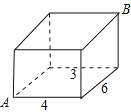
【题目】如图,是一个长宽高分别为6,4,3的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体表面到长方体上和A处相对的顶点B处吃食物,那么它需要爬行的最短路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,2).
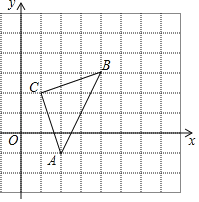
(1)写出点A,B的坐标:A( )、B( );
(2)判断△ABC的形状 ;计算△ABC的面积是 .
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到![]() ,则
,则![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ( ),
( ),![]() ( ),
( ),![]() ( ).
( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
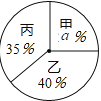
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
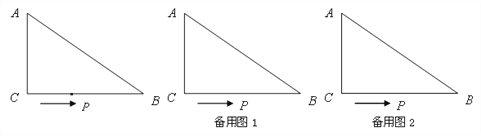
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1) 当t=1时,求△ACP的面积
(2) t为何值时,线段AP是∠CAB的平分线?
(3) 请利用备用图2继续探索:当t为何值时,△ACP是以AC为腰的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,图中AB=AC,AD=AE,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连结DC.
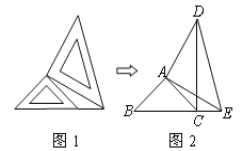
(1)图2中的全等三角形是_______________,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com