
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,2).
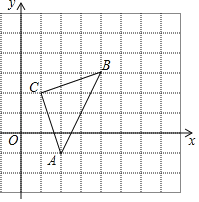
(1)写出点A,B的坐标:A( )、B( );
(2)判断△ABC的形状 ;计算△ABC的面积是 .
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到![]() ,则
,则![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ( ),
( ),![]() ( ),
( ),![]() ( ).
( ).
【答案】(1)(2,1),(4,3);(2)等腰直角三角形,5;(3)(0,0)、(2,4)、(1,3).
【解析】
(1)根据直角坐标系的特点写出点的坐标;
(2)求出AC,BC,AB,利用勾股定理逆定义判断三角形形状,根据等腰直角三角形面积公式求△ABC的面积;
(3)分别将点A、B、C先向左平移2个单位长度,再向上平移1个单位长度,得到点A′、B′、C′,然后顺次连接得到![]() ,写出坐标即可.
,写出坐标即可.
解:(1)由A,B在直角坐标系中的位置可知:A(2,1),B(4,3);
(2)∵AC=BC=![]() ,AB=
,AB=![]() ,
,
∴AC2+BC2=AB2,
∴△ABC的形状是等腰直角三角形,
∴S△ABC=![]() ,
,
(3)![]() 的位置如图所示:
的位置如图所示:
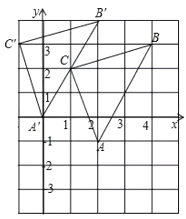
∴A′(0,0)、B′(2,4)、C′(1,3).
故答案为:(1)(2,1),(4,3);(2)等腰直角三角形,5;(3)(0,0)、(2,4)、(1,3).


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
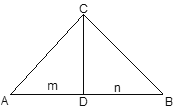
【题目】如图,已知△ABC中,∠ACB=90°,过C点作CD⊥AB,垂足为D,且AD=m,BD= n,AC2:BC2=2:1,又关于x的方程![]() x2-2(n-1)x+m2-12=0,两实数根的差的平方小于192,
x2-2(n-1)x+m2-12=0,两实数根的差的平方小于192,
求:m,n为整数时,一次函数y=mx+n的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A′B′C′关于点P成中心对称,则点A′的坐标为( )

A. (﹣4,﹣5) B. (﹣5,﹣4) C. (﹣3,﹣4) D. (﹣4,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
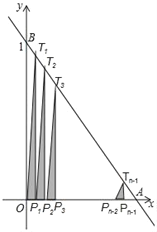
【题目】如图,直线y=﹣x+1与两坐标轴分别交于A,B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn﹣1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn﹣1,用S1,S2,S3,…,Sn﹣1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn﹣1Pn﹣2Pn﹣1的面积,则S1+S2+S3+…+Sn﹣1=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图①是一个长为2m,宽为2n的长方形.沿图中虚线把它分割成四块完全相同的小长方形,然后按图②的形状拼成一个正方形.
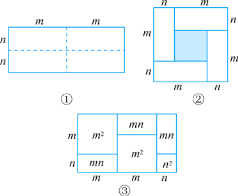
(1)求图②中阴影部分的面积.
(2)观察图②,发现三个代数式(m+n)2,(m-n)2,mn之间的等量关系是 .
(3)若x+y=-6,xy=2.75,求x-y的值.
(4)观察图③,你能得到怎样的代数恒等式?
(5)试画出一个几何图形,使它的面积能表示代数恒等式(m+n)(m+3n)=m2+4mn+3n2.
查看答案和解析>>
科目:初中数学 来源: 题型:
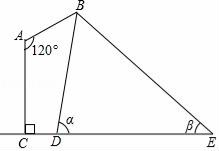
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B
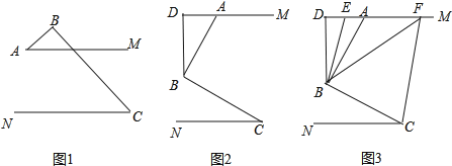
(1)如图1,直接写出∠A和∠C之间的数量关系;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E.F在DM上,连接BE.BF.CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠ABF=2∠ABE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案

(1)填写下表:
图形序号 | ① | ② | ③ | …… | ⑧ |
每个图案中小棒的数量 | 6 | 11 | …… |
(2)请填写出第![]() 个图案中小棒的数量(用含
个图案中小棒的数量(用含![]() 的代数式表示);
的代数式表示);
(3)第30个图案中小棒有多少根?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com