
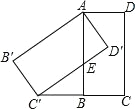
【题目】如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点 C的对应点 C′恰好落在CB的延长线上,边AB交边 C′D′于点E.
(1)求证:BC=BC′;
(2)若 AB=2,BC=1,求AE的长.
【答案】(1)证明见解析;(2)AE=![]() .
.
【解析】
(1)连结 AC、AC′,根据矩形的性质得到∠ABC=90°,即 AB⊥CC′, 根据旋转的性质即可得到结论;
(2)根据矩形的性质得到 AD=BC,∠D=∠ABC′=90°,根据旋转的性质得到 BC′=AD′,AD=AD′,证得 BC′=AD′,根据全等三角形的性质得到 BE=D′E,设 AE=x,则 D′E=2﹣x,根据勾股定理列方程即可得到结论.
解::(1)连结 AC、AC′,
∵四边形 ABCD为矩形,
∴∠ABC=90°,即 AB⊥CC′,
∵将矩形 ABCD 绕点A顺时针旋转,得到矩形 AB′C′D′,
∴AC=AC′,
∴BC=BC′;
(2)∵四边形 ABCD 为矩形,
∴AD=BC,∠D=∠ABC′=90°,
∵BC=BC′,
∴BC′=AD′,
∵将矩形 ABCD 绕点 A 顺时针旋转,得到矩形 AB′C′D′,
∴AD=AD′,
∴BC′=AD′,
在△AD′E 与△C′BE中
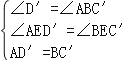
∴△AD′E≌△C′BE,
∴BE=D′E,
设 AE=x,则 D′E=2﹣x,
在 Rt△AD′E 中,∠D′=90°,
由勾定理,得 x2﹣(2﹣x)2=1,
解得 x=![]() ,
,
∴AE= ![]() .
.


科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形W和点P,给出如下定义:F为图形W上任意一点,将P,F两点间距离的最小值记为m,最大值记为M,称M与m的差为点P到图形W的“差距离”,记作d(P,W),即d(P,W)=M-m,已知点A(2,1),B(-2,1)
(1)求d(O,AB);
(2)点C为直线y=1上的一个动点,当d(C,AB)=1时,点C的横坐标是 ;
(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点,当d(D,AB)≤2时,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一列数:![]() ,
,![]() ,0,-22,-(+2),-(-4),请回答下列问题:
,0,-22,-(+2),-(-4),请回答下列问题:
(1)其中非负整数是_______________;(2)到原点距离相等的数是________________;
(3)画出数轴,并在数轴上表示这一列数,再用“<”连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=![]() 的图象上,则k的值为__.
的图象上,则k的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
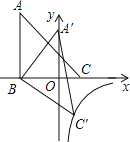
【题目】某课外研究小组为了解学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名同学的兴趣爱好(每人只能选其中一项),并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
(1)在这次考察中一共调查了 名学生,请补全条形统计图;
(2)被调查同学中恰好有5名学来自初一12班,其中有2名同学选择了篮球,有3名同学选择了乒乓球,曹老师打算从这5名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好为一人选择篮球、一人选择乒乓球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(3.6,a),B(2,2),C(b,3.4),D(8,6),则![]() 的值为( )
的值为( )

A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沙坪坝区政府决定从2014年11月起到2016年底,两年时间创建成为国家卫生城区,辖区内企业的污水处理通常有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理,某企业每月的污水量均为2500吨,数量巨大需要两种处理方式同时进行.由于企业自身设备老化等问题,2015年每月自身处理污水量y(吨)与月份x(x取整数)之间满足的函数关系式为y=2500﹣100x,该企业自身处理每吨污水的成本为4元,其余部分由污水厂统一处理,污水厂收取企业每吨污水处理费10元
(1)该企业2015年哪几个月用于污水处理的费用不超过12000元?
(2)2016年以来,由于该企业自建污水处理设备的全面运行,该企业决定扩大产能并将所有污水全部自身处理,估计扩大产能后2016年每月的污水量都将在2015年每月的基础上增加a%,同时每吨污水处理的费用将在每吨4元的基础上增加5(a﹣30)%,为鼓励节能降耗,减轻企业负担,财政对企业处理污水的费用进行50%的补助,若该企业每月的污水处理费用为8437.5元,请计算出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】树叶有关的问题
如图,一片树叶的长是指沿叶脉方向量出的最长部分的长度(不含叶柄),树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度,树叶的长宽比是指树叶的长与树叶的宽的比值。

某同学在校园内随机收集了A树、B树、C树三棵的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据,计算长宽比,理如下:
表1 A树、B树、C树树叶的长宽比统计表
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
A树树叶的长宽比 | 4.0 | 4.9 | 5.2 | 4.1 | 5.7 | 8.5 | 7.9 | 6.3 | 7.7 | 7.9 |
B树树叶的长宽比 | 2.5 | 2.4 | 2.2 | 2.3 | 2.0 | 1.9 | 2.3 | 2.0 | 1.9 | 2.0 |
C树树叶的长宽比 | 1.1 | 1.2 | 1.2 | 0.9 | 1.0 | 1.0 | 1.1 | 0.9 | 1.0 | 1.3 |
表1 A树、B树、C树树叶的长宽比的平均数、中位数、众数、方差统计表
平均数 | 中位数 | 众数 | 方差 | |
A树树叶的长宽比 | 6.2 | 6.0 | 7.9 | 2.5 |
B树树叶的长宽比 | 2.2 | 0.38 | ||
C树树叶的长宽比 | 1.1 | 1.1 | 1.0 | 0.02 |
A树、B树、C树树叶的长随变化的情况

解决下列问题:
(1)将表2补充完整;
(2)①小张同学说:“根据以上信息,我能判断C树树叶的长、宽近似相等。”
②小李同学说:“从树叶的长宽比的平均数来看,我认为,下图的树叶是B树的树叶。”
![]()
请你判断上面两位同学的说法中,谁的说法是合理的,谁的说法是不合理的,并给出你的理由;
(3)现有一片长103cm,宽52cm的树叶,请将该树叶的数用“★”表示在图1中,判断这片树叶更可能来自于A、B、C中的哪棵树?并给出你的理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com