
ЎѕМвДїЎїЙіЖє°УЗшХюё®ѕц¶ЁґУ2014Дк11ФВЖрµЅ2016ДкµЧЈ¬БЅДкК±јдґґЅЁіЙОЄ№ъјТОАЙъіЗЗшЈ¬ПЅЗшДЪЖуТµµДОЫЛ®ґ¦АнНЁіЈУРБЅЦЦ·ЅКЅЈ¬Т»ЦЦКЗКдЛНµЅОЫЛ®і§ЅшРРјЇЦРґ¦АнЈ¬БнТ»ЦЦКЗНЁ№эЖуТµµДЧФЙнЙи±ёЅшРРґ¦АнЈ¬ДіЖуТµГїФВµДОЫЛ®БїѕщОЄ2500¶ЦЈ¬КэБїѕЮґуРиТЄБЅЦЦґ¦Ан·ЅКЅН¬К±ЅшРРЈ®УЙУЪЖуТµЧФЙнЙи±ёАП»ЇµИОКМвЈ¬2015ДкГїФВЧФЙнґ¦АнОЫЛ®БїyЈЁ¶ЦЈ©УлФВ·ЭxЈЁxИЎХыКэЈ©Ц®јдВъЧгµДєЇКэ№ШПµКЅОЄy=2500©Ѓ100xЈ¬ёГЖуТµЧФЙнґ¦АнГї¶ЦОЫЛ®µДіЙ±ѕОЄ4ФЄЈ¬ЖдУаІї·ЦУЙОЫЛ®і§НіТ»ґ¦АнЈ¬ОЫЛ®і§КХИЎЖуТµГї¶ЦОЫЛ®ґ¦Ан·С10ФЄ
ЈЁ1Ј©ёГЖуТµ2015ДкДДјёёцФВУГУЪОЫЛ®ґ¦АнµД·СУГІ»і¬№э12000ФЄЈї
ЈЁ2Ј©2016ДкТФАґЈ¬УЙУЪёГЖуТµЧФЅЁОЫЛ®ґ¦АнЙи±ёµДИ«ГжФЛРРЈ¬ёГЖуТµѕц¶ЁА©ґуІъДЬІўЅ«ЛщУРОЫЛ®И«ІїЧФЙнґ¦АнЈ¬№АјЖА©ґуІъДЬєу2016ДкГїФВµДОЫЛ®Бї¶јЅ«ФЪ2015ДкГїФВµД»щґЎЙПФцјУa%Ј¬Н¬К±Гї¶ЦОЫЛ®ґ¦АнµД·СУГЅ«ФЪГї¶Ц4ФЄµД»щґЎЙПФцјУ5ЈЁa©Ѓ30Ј©%Ј¬ОЄ№ДАшЅЪДЬЅµєДЈ¬јхЗбЖуТµёєµЈЈ¬ІЖХю¶ФЖуТµґ¦АнОЫЛ®µД·СУГЅшРР50%µДІ№ЦъЈ¬ИфёГЖуТµГїФВµДОЫЛ®ґ¦Ан·СУГОЄ8437.5ФЄЈ¬ЗлјЖЛгіцaµДЦµЈ®
Ўѕґр°ёЎїЈЁ1Ј©ёГЖуТµ2015ДкТ»Ўў¶юЎўИэФВУГУЪОЫЛ®ґ¦АнµД·СУГІ»і¬№э12000ФЄЈ»ЈЁ2Ј©aµДЦµОЄ35Ј®
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁ1Ј©ёщѕЭОЫЛ®ґ¦АнЧЬ·СУГ=4ЎБЖуТµЧФЙнґ¦АнОЫЛ®¶ЦКэ+10ЎБОЫЛ®і§ґ¦АнОЫЛ®¶ЦКэЅбєПЧЬ·СУГІ»і¬№э12000ФЄЈ¬јґїЙµГіц№ШУЪxµДТ»ФЄТ»ґОІ»µИКЅЈ¬ЅвЦ®јґїЙµГіцxµДИЎЦµ·¶О§Ј¬ФЩёщѕЭxОЄХэХыКэјґїЙµГіцЅбВЫЈ»
ЈЁ2Ј©ёщѕЭОЫЛ®ґ¦Ан·СУГ=ґ¦АнГї¶ЦОЫЛ®µД·СУГЎБОЫЛ®ЧЬБїјґїЙµГіц№ШУЪaµДТ»ФЄ¶юґО·ЅіМЈ¬ЅвЦ®јґїЙµГіцЅбВЫЈ®
КФМвЅвОцЈєЅвЈєЈЁ1Ј©ёщѕЭМвТвµГЈє4ЈЁ2500©Ѓ100xЈ©+10[2500©ЃЈЁ2500©Ѓ100xЈ©]ЎЬ12000Ј¬ХыАнµГЈє600x+10000ЎЬ12000Ј¬ЅвµГЈєxЎЬ![]() Ј®ЎЯxОЄХэХыКэЈ¬Ўаx=1Ўў2Ўў3Ј¬ЎаёГЖуТµ2015ДкТ»Ўў¶юЎўИэФВУГУЪОЫЛ®ґ¦АнµД·СУГІ»і¬№э12000ФЄЈ®
Ј®ЎЯxОЄХэХыКэЈ¬Ўаx=1Ўў2Ўў3Ј¬ЎаёГЖуТµ2015ДкТ»Ўў¶юЎўИэФВУГУЪОЫЛ®ґ¦АнµД·СУГІ»і¬№э12000ФЄЈ®
ЈЁ2Ј©ёщѕЭМвТвµГЈє2500ЈЁ1+a%Ј©ЎБ4[1+5ЈЁa©Ѓ30Ј©%]=8437.5ЎБ2Ј¬ХыАнµГЈєa2+90a©Ѓ4375=0Ј¬ЅвµГЈєa=35»тa=©Ѓ125ЈЁЙбИҐЈ©Ј®
ґрЈєИфёГЖуТµГїФВµДОЫЛ®ґ¦Ан·СУГОЄ8437.5ФЄЈ¬aµДЦµОЄ35Ј®


 ФД¶БїміµПµБРґр°ё
ФД¶БїміµПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬DОЄABЙПТ»µгЈ¬ЎчACEЎХЎчBCDЈ¬AD2+DB2=DE2Ј¬КФЕР¶ПЎчABCµДРОЧґЈ¬ІўЛµГчАнУЙЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЎСOЦРЈ¬Ц±ѕ¶CDґ№Ц±УЪІ»№эФІРДOµДПТABЈ¬ґ№ЧгОЄµгNЈ¬Б¬ЅУACЈ¬µгEФЪABЙПЈ¬ЗТAE=CEЈ¬№эµгBЧчЎСOµДЗРПЯЅ»ECµДСУі¤ПЯУЪµгPЈ®
ЈЁ1Ј©ЗуЦ¤ЈєAC2=AEABЈ»
ЈЁ2Ј©КФЕР¶ПPBУлPEКЗ·сПаµИЈ¬ІўЛµГчАнУЙЈ»
ЈЁ3Ј©ЙиЎСOµД°лѕ¶ОЄ4Ј¬NОЄOCµДЦРµгЈ¬µгQФЪЎСOЙПЈ¬ЗуПЯ¶ОPQµДЧоРЎЦµЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Ѕ«ѕШРОABCDИЖµгAЛіК±ХлРэЧЄЈ¬µГµЅѕШРОABЎдCЎдDЎдЈ¬µг CµД¶ФУ¦µг CЎдЗЎєГВдФЪCBµДСУі¤ПЯЙПЈ¬±ЯABЅ»±Я CЎдDЎдУЪµгEЈ®
ЈЁ1Ј©ЗуЦ¤ЈєBCЈЅBCЎдЈ»
ЈЁ2Ј©Иф ABЈЅ2Ј¬BCЈЅ1Ј¬ЗуAEµДі¤Ј®
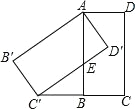
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДі№¤і§Т»ёціµјд№¤ИЛјЖ»®Т»ЦЬЖЅѕщГїМмЙъІъБгјю300ёцЈ¬КµјКГїМмЙъІъБїУлјЖ»®ГїМмЙъІъБїПа±ИУРОуІо.Из±нКЗХвёціµјд№¤ИЛФЪДіТ»ЦЬГїМмµДБгјюЙъІъЗйїцЈ¬і¬јЖ»®ЙъІъБїОЄХэЎўІ»ЧгјЖ»®ЙъІъБїОЄёє.(µҐО»Јєёц)
К±јд | ЦЬТ» | ЦЬ¶ю | ЦЬИэ | ЦЬЛД | ЦЬОе | ЦЬБщ | ЦЬИХ |
ОуІо | +10 | Ј15 | Ј6 | +12 | Ј10 | +18 | Ј11 |
(1)ЙъІъБгјюКэБїЧоЙЩµДТ»Мм±ИЧо¶аµДТ»МмЙЩЙъІъ______ёцБгјюЈ»
(2)ИфЙъІъТ»ёцБгјюїЙµГАыИу5ФЄЈ¬ФтХвёціµјдµД№¤ИЛФЪХвТ»ЦЬОЄ№¤і§Т»№ІґшАґБЛ¶аЙЩАыИуЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФД¶БПВБРЅвМв№эіМЈє
јЖЛгЈє(Ј5)ЎВ![]() ЎБ20.
ЎБ20.
ЅвЈєФКЅЈЅ(Ј5)ЎВ![]() ЎБ20ЎЎ(µЪТ»ІЅ)
ЎБ20ЎЎ(µЪТ»ІЅ)
ЈЅ(Ј5)ЎВ(Ј1)ЎЎ(µЪ¶юІЅ)
ЈЅЈ5.ЎЎЎЎЎЎ(µЪИэІЅ)
(1)ЙПКцЅвМв№эіМЦРУРБЅґ¦ґнОуЈє
µЪТ»ґ¦КЗµЪ________ІЅЈ¬ґнОуµДФТтКЗ__________________________Ј»
µЪ¶юґ¦КЗµЪ________ІЅЈ¬ґнОуµДФТтКЗ_______________________Ј®
(2)°СХэИ·µДЅвМв№эіМРґіцАґЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄБЛјУЗї№«ГсµДЅЪЛ®ТвК¶Ј¬єПАнАыУГЛ®ЧКФґЈ¬ДіКРІЙУГјЫёсµчїШКЦ¶ОґпµЅЅЪЛ®µДДїµДЈ®ёГКРЧФАґЛ®КХ·СјЫёсјыјЫДї±нЈ®

ЧўЈєЛ®·С°ґФВЅбЛгЈ¬І»Чг1Бў·ЅГЧµДІ»КХ·СЈ®ИфДі»§ѕУГс1ФВ·ЭУГЛ®8Бў·ЅГЧЈ¬ФтУ¦Ѕ»Л®·СЈє2ЎБ6Ј«4ЎБ(8Ј6)ЈЅ20(ФЄ)Ј®
(1)ИфёГ»§ѕУГс2ФВ·ЭЅ»Л®·С16ФЄЈ¬јЖЛгёГ»§ѕУГс2ФВ·ЭµДУГЛ®БїЈ»
(2)ИфёГ»§ѕУГс3ФВ·ЭУГЛ®12.5Бў·ЅГЧЈ¬ФтУ¦Ѕ»Л®·С¶аЙЩФЄЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТ»Мъ°фУыНЁ№эТ»ёцЦ±ЅЗЧЯАИЈ®ИзНјЈ¬КЗёГМъ°фЅф°¤ЧЕЗЅЅЗEНЁ№эК±µДБЅёцМШКвО»ЦГЈєµ±Мъ°фО»УЪABО»ЦГК±Ј¬ЛьУлЗЅГжOGЛщіЙµДЅЗЎПABO![]() 51Ўг18ЎдЈ»µ±Мъ°фµЧ¶ЛBПтЙП»¬¶Ї1m(јґBD
51Ўг18ЎдЈ»µ±Мъ°фµЧ¶ЛBПтЙП»¬¶Ї1m(јґBD![]() 1m)µЅґпCDО»ЦГК±Ј¬ЛьУлЗЅГжOGЛщіЙµДЅЗЎПCDO
1m)µЅґпCDО»ЦГК±Ј¬ЛьУлЗЅГжOGЛщіЙµДЅЗЎПCDO![]() 60ЎгЈ¬ЗуМъ°фµДі¤Ј®ЈЁІОїјКэѕЭЈєsin51Ўг18Ўд
60ЎгЈ¬ЗуМъ°фµДі¤Ј®ЈЁІОїјКэѕЭЈєsin51Ўг18Ўд![]() 0.780Ј¬cos51Ўг18Ўд
0.780Ј¬cos51Ўг18Ўд![]() 0.625Ј¬tan51Ўг18Ўд
0.625Ј¬tan51Ўг18Ўд![]() 1.248Ј©
1.248Ј©

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї№ШУЪ![]() µД·ЅіМ
µД·ЅіМ![]() µДЛщУРёщ¶јКЗ±И1РЎµДХэКµКэЈ¬ФтКµКэ
µДЛщУРёщ¶јКЗ±И1РЎµДХэКµКэЈ¬ФтКµКэ![]() µДИЎЦµ·¶О§КЗ_______________.
µДИЎЦµ·¶О§КЗ_______________.
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com