
【题目】如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE,过点B作⊙O的切线交EC的延长线于点P.
(1)求证:AC2=AEAB;
(2)试判断PB与PE是否相等,并说明理由;
(3)设⊙O的半径为4,N为OC的中点,点Q在⊙O上,求线段PQ的最小值.

【答案】(1)(2)见解析;(3)线段PQ的最小值是![]() ﹣4.
﹣4.
【解析】分析:(1)证明△AEC∽△ACB,列比例式可得结论;
(2)如图2,证明∠PEB=∠COB=∠PBN,根据等角对等边可得:PB=PE;
(3)如图3,先确定线段PQ的最小值时Q的位置:因为OQ为半径,是定值4,则PQ+OQ的值最小时,PQ最小,当P、Q、O三点共线时,PQ最小,先求AE的长,从而得PB的长,最后利用勾股定理求OP的长,与半径的差就是PQ的最小值.
详解:证明:(1)如图1,连接BC,
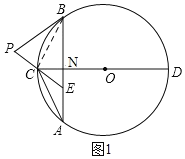
∵CD为⊙O的直径,AB⊥CD,
∴![]() =
=![]() ,
,
∴∠A=∠ABC,
∵EC=AE,
∴∠A=∠ACE,
∴∠ABC=∠ACE,
∵∠A=∠A,
∴△AEC∽△ACB,
∴![]()
∴![]()
(2)PB=PE,理由是:
如图2,连接OB,
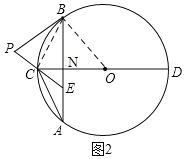
∵PB为⊙O的切线,
∴OB⊥PB,
∴![]()
∴![]()
∵![]()
∴∠PBN=∠COB,
∵∠PEB=∠A+∠ACE=2∠A,
∠COB=2∠A,
∴∠PEB=∠COB,
∴∠PEB=∠PBN,
∴PB=PE;
(3)如图3,∵N为OC的中点,
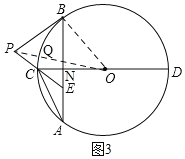
∴![]()
Rt△OBN中, ![]()
∴![]()
∵OC=OB,
∴△OCB为等边三角形,
∵Q为⊙O任意一点,
连接PQ、OQ,
因为OQ为半径,是定值4,
则PQ+OQ的值最小时,PQ最小,
当P、Q、O三点共线时,PQ最小,
∴Q为OP与⊙O的交点时,PQ最小,
![]()
∴![]()
![]()
∴△PBE是等边三角形,
Rt△OBN中, ![]()
∴![]()
设AE=x,则CE=x, ![]()
Rt△CNE中, ![]()
![]()
∴![]()
Rt△OPB中, ![]()
∴![]()
则线段PQ的最小值是![]()


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的分式方程![]() ①和一元二次方程
①和一元二次方程![]() ②中,m为常数,方程①的根为非负数.
②中,m为常数,方程①的根为非负数.
(1)求m的取值范围;
(2)若方程②有两个整数根x1、x2,且m为整数,求方程②的整数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某司机在东西路上开车接送乘客,他早晨从A地出发,(去向东的方向正方向),到晚上送走最后一位客人为止,他一天行驶的的里程记录如下(单位:㎞)
+10 ,— 5, —15 ,+ 30 ,—20 ,—16 ,+ 14
(1) 若该车每百公里耗油 3 L ,则这车今天共耗油 多少升?
(2) 据记录的情况,你能否知道该车送完最后一个乘客是,他在A地的什么方向?距A地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一列数:![]() ,
,![]() ,0,-22,-(+2),-(-4),请回答下列问题:
,0,-22,-(+2),-(-4),请回答下列问题:
(1)其中非负整数是_______________;(2)到原点距离相等的数是________________;
(3)画出数轴,并在数轴上表示这一列数,再用“<”连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为15,OC边长为3.

(1)数轴上点A表示的数为 .
(2)将长方形OABC沿数轴水平方向移动,移动后的长方形记为O′A′B′C′(O、A、B、C对应点分别为O′、A′、B′、C′),移动后的长方形O′A′B′C′与原长方形OABC重叠部分的周长记为L.
①当L=10时,移动的距离为 ;
②当L恰好等于原长方形OABC周长的一半时,数轴上点A′表示的数为 .
③设点A的移动距离AA′=x.若D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=![]() 的图象上,则k的值为__.
的图象上,则k的值为__.
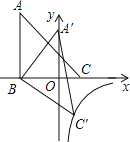
查看答案和解析>>
科目:初中数学 来源: 题型:
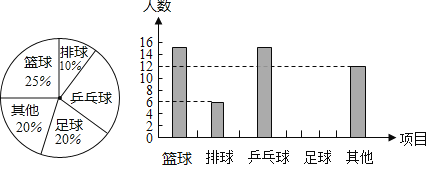
【题目】某课外研究小组为了解学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名同学的兴趣爱好(每人只能选其中一项),并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
(1)在这次考察中一共调查了 名学生,请补全条形统计图;
(2)被调查同学中恰好有5名学来自初一12班,其中有2名同学选择了篮球,有3名同学选择了乒乓球,曹老师打算从这5名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好为一人选择篮球、一人选择乒乓球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沙坪坝区政府决定从2014年11月起到2016年底,两年时间创建成为国家卫生城区,辖区内企业的污水处理通常有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理,某企业每月的污水量均为2500吨,数量巨大需要两种处理方式同时进行.由于企业自身设备老化等问题,2015年每月自身处理污水量y(吨)与月份x(x取整数)之间满足的函数关系式为y=2500﹣100x,该企业自身处理每吨污水的成本为4元,其余部分由污水厂统一处理,污水厂收取企业每吨污水处理费10元
(1)该企业2015年哪几个月用于污水处理的费用不超过12000元?
(2)2016年以来,由于该企业自建污水处理设备的全面运行,该企业决定扩大产能并将所有污水全部自身处理,估计扩大产能后2016年每月的污水量都将在2015年每月的基础上增加a%,同时每吨污水处理的费用将在每吨4元的基础上增加5(a﹣30)%,为鼓励节能降耗,减轻企业负担,财政对企业处理污水的费用进行50%的补助,若该企业每月的污水处理费用为8437.5元,请计算出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |

请根据以上信息解答下列问题:
(1)填空:m= ______ ,n= ______ ;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com