
【题目】树叶有关的问题
如图,一片树叶的长是指沿叶脉方向量出的最长部分的长度(不含叶柄),树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度,树叶的长宽比是指树叶的长与树叶的宽的比值。

某同学在校园内随机收集了A树、B树、C树三棵的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据,计算长宽比,理如下:
表1 A树、B树、C树树叶的长宽比统计表
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
A树树叶的长宽比 | 4.0 | 4.9 | 5.2 | 4.1 | 5.7 | 8.5 | 7.9 | 6.3 | 7.7 | 7.9 |
B树树叶的长宽比 | 2.5 | 2.4 | 2.2 | 2.3 | 2.0 | 1.9 | 2.3 | 2.0 | 1.9 | 2.0 |
C树树叶的长宽比 | 1.1 | 1.2 | 1.2 | 0.9 | 1.0 | 1.0 | 1.1 | 0.9 | 1.0 | 1.3 |
表1 A树、B树、C树树叶的长宽比的平均数、中位数、众数、方差统计表
平均数 | 中位数 | 众数 | 方差 | |
A树树叶的长宽比 | 6.2 | 6.0 | 7.9 | 2.5 |
B树树叶的长宽比 | 2.2 | 0.38 | ||
C树树叶的长宽比 | 1.1 | 1.1 | 1.0 | 0.02 |
A树、B树、C树树叶的长随变化的情况

解决下列问题:
(1)将表2补充完整;
(2)①小张同学说:“根据以上信息,我能判断C树树叶的长、宽近似相等。”
②小李同学说:“从树叶的长宽比的平均数来看,我认为,下图的树叶是B树的树叶。”
![]()
请你判断上面两位同学的说法中,谁的说法是合理的,谁的说法是不合理的,并给出你的理由;
(3)现有一片长103cm,宽52cm的树叶,请将该树叶的数用“★”表示在图1中,判断这片树叶更可能来自于A、B、C中的哪棵树?并给出你的理由。
【答案】(1)2.1,2.0;(2)小张同学的说法是合理的,小李学同的说法是不合理;(3)B树;
【解析】
(1)根据中位数和众数的定义,由表中的数据求出B树树叶的长宽比的中位数和众数即可;
(2)根据表中数据,求出C树树叶的长宽比的近似值,从而判断小张的说法,根据所给树叶的长宽比,判断小李的说法即可;
(3)根据树叶的长和宽在图中用★标出该树叶,根据树叶的长宽比判断该树叶来自哪棵树即可.
解(1)将这10片B树树叶的长宽比从小到大排列为:1.9,1.9,2.0,2.0,2.0,2.2,2.3,2.3,2.4,2.5,处在中间位置的两个数为2.0,2.2,
∴中位数为(2.0+2.2)÷2=2.1;
∵2.0出现了3次,出现的次数最多,
∴众数为2.0.
平均数 | 中位数 | 众数 | 方差 | |
A树树叶的长宽比 | ||||
B树树叶的长宽比 | 2.1 | 2.0 | ||
C树树叶的长宽比 |
(2)小张同学的说法是合理的,小李同学的说法是不合理的.
理由如下:由表中的数据可知C树叶的长宽比近似于1,故小张的说法正确;
由树叶的长度和宽度可知该树叶的长宽比近似于6,所以该树叶是A树的树叶,故小李的说法错误;
(3)图1中,★表示这片树叶的数据,这片树叶来自B树;
这块树叶的长宽比为103:52≈2,所以这片树叶来自B树.



 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
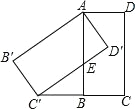
【题目】如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点 C的对应点 C′恰好落在CB的延长线上,边AB交边 C′D′于点E.
(1)求证:BC=BC′;
(2)若 AB=2,BC=1,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一铁棒欲通过一个直角走廊.如图,是该铁棒紧挨着墙角E通过时的两个特殊位置:当铁棒位于AB位置时,它与墙面OG所成的角∠ABO![]() 51°18′;当铁棒底端B向上滑动1m(即BD
51°18′;当铁棒底端B向上滑动1m(即BD![]() 1m)到达CD位置时,它与墙面OG所成的角∠CDO
1m)到达CD位置时,它与墙面OG所成的角∠CDO![]() 60°,求铁棒的长.(参考数据:sin51°18′
60°,求铁棒的长.(参考数据:sin51°18′![]() 0.780,cos51°18′
0.780,cos51°18′![]() 0.625,tan51°18′
0.625,tan51°18′![]() 1.248)
1.248)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长和宽分别是a,b的长方形的四个角都剪去一个边长为x的正方形,折叠后,做成一无盖的盒子(单位:cm).
(1)用a,b,x表示纸片剩余部分的面积;
(2)用a,b,x表示盒子的体积;
(3)当a=10,b=8且剪去的每一个小正方形的面积等于4 cm2时,求剪去的每一个正方形的边长及所做成的盒子的体积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,对角线AC,BD交于点O,E是AD上任意一点,连接EO并延长,交BC于点F,连接AF,CE.
中,对角线AC,BD交于点O,E是AD上任意一点,连接EO并延长,交BC于点F,连接AF,CE.

(1)求证:四边形AFCE是平行四边形;
(2)若![]() ,
,![]() °,
°,![]() .
.
①直接写出![]() 的边BC上的高h的值;
的边BC上的高h的值;
②当点E从点D向点A运动的过程中,下面关于四边形AFCE的形状的变化的说法中,正确的是
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形→正方形→平行四边形
C.平行四边形→菱形→平行四边形→菱形→平行四边形
D.平行四边形→菱形→平行四边形→矩形→平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有A、B两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室阅读.
(1)下列事件中,是必然事件的为( )
A.甲、乙同学都在A阅览室 B.甲、乙、丙同学中至少两人在A阅览室
C.甲、乙同学在同一阅览室 D.甲、乙、丙同学中至少两人在同一阅览室
(2)用画树状图的方法求甲、乙、丙三名学生在同一阅览室阅读的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的边OA在x轴上,将平行四边形沿对角线AC对折,AO的对应线段为AD,且点D,C,O在同一条直线上,AD与BC交于点E.

(1)求证:△ABC≌△CDA.
(2)若直线AB的函数表达式为![]() ,求三角线ACE的面积.
,求三角线ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD。理由如下:

∵∠1=∠2(已知)
且∠1=∠4( )
∴∠2=∠4(等量代换)
∴CE∥BF( )
∴∠ =∠BFD( )
又∵∠B=∠C(已知)
∴ (等量代换)
∴AB∥CD( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com