
【题目】如图,在平面直角坐标系中,边长为4的等边![]() 的边
的边![]() 在
在![]() 轴的负半轴上,反比例函数
轴的负半轴上,反比例函数![]() 的图象经过
的图象经过![]() 边的中点
边的中点![]() ,且与
,且与![]() 边交于点
边交于点![]() .
.

(1)求![]() 的值;
的值;
(2)连接![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(3)若直线![]() 与直线
与直线![]() 平行,且与
平行,且与![]() 的边有交点,直接写出
的边有交点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 3;(3)
3;(3)![]() .
.
【解析】
(1)过点![]() 作
作![]() 于
于![]() ,根据等边三角形的性质可求出点C的坐标,把点C的坐标代入反比例函数
,根据等边三角形的性质可求出点C的坐标,把点C的坐标代入反比例函数![]() 即可求出k的值;
即可求出k的值;
(2)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() .再根据等边三角形的性质可求得AF,BF,从而求出点A的坐标.再用待定系数法求出直线OA的解析式,让反比例函数解析 式与直线OA的解析式联立解方程组求出点D的坐标,三角形OCD的面积=四边形ODCE的面积-三角形OCE的面积.从而得到求解.
.再根据等边三角形的性质可求得AF,BF,从而求出点A的坐标.再用待定系数法求出直线OA的解析式,让反比例函数解析 式与直线OA的解析式联立解方程组求出点D的坐标,三角形OCD的面积=四边形ODCE的面积-三角形OCE的面积.从而得到求解.
(3)由图形可知当![]() 过点C时n有最大值,当
过点C时n有最大值,当![]() 时n有最小值.
时n有最小值.
(1)如图1,过点![]() 作
作![]() 于
于![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∵![]() 是
是![]() 中点,
中点,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
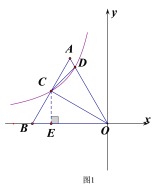
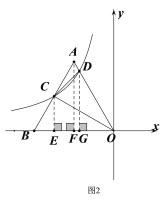
(2)如图2.过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() .
.
则![]() ,
,![]() ,
,
∴![]() ,
,
设直线![]() 解析式为
解析式为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)可知反比例函数解析式为![]() ,
,
联立方程组: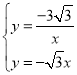 ,
,
解得: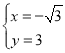 或
或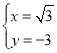 (舍),
(舍),
∴![]() ,
,
∴![]()
![]()
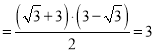 .
.
(3)![]() .理由如下:
.理由如下:
∵![]() ,
,![]() ,
,
∴![]() =1.
=1.
∵直线![]() 与直线
与直线![]() 平行,
平行,
∴m=1.
∴直线![]() 解析式为
解析式为![]() .
.
∴把![]() 代入
代入![]() ,得:
,得:
n=![]() .
.
把![]() 代入
代入![]() ,得:
,得:
n=0.
∴![]()


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0),则下面的四个结论,其中正确的个数为( )
①2a+b=0②4a﹣2b+c<0③ac>0④当y>0时,﹣1<x<4
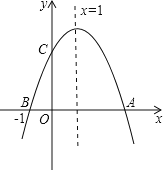
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.
S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,每件成本为50元,如果按每件60元出售,可销售800件;如果每件提价5元出售,其销售量就减少100件,如果商场销售这批衬衫要获利润12000元,又使顾客获得更多的优惠,那么这种衬衫售价应定为多少元?
(1)设提价了![]() 元,则这种衬衫的售价为___________元,销售量为____________件.
元,则这种衬衫的售价为___________元,销售量为____________件.
(2)列方程完成本题的解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1m的竹竿的影长为0.5m,同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,其中,落在墙壁上的影长为0.8m,落在地面上的影长为4.4m,则树的高为_______m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37 34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38 34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据,解答以下问题:
(1)小彬按“组距为5”列出了如下的频数分布表,每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图:
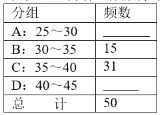
(2)在(1)的基础上,小彬又画出了如图所示的扇形统计图,图中B组所对的圆心角的度数为 ;
(3)根据(1)中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征.
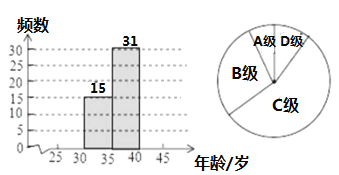
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班的同学踊跃为“雅安芦山地震”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但生活委员不小心把墨水滴在统计表上,部分数据看不清楚.
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?
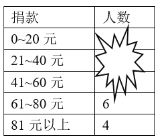
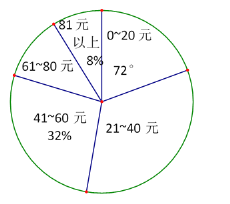
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com