
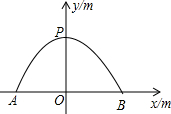
 一个横截面为抛物线形的隧道底部宽AB为12m,最大高度OP为6m,如图,车辆双向通行,规定车辆必须在中心线右侧,距道路边缘2m这一范围内行驶,并保持车辆顶部与隧道有不少于0.4m的空隙,现以AB中点O为原点,AB所在直线为x轴建立直角坐标系.
一个横截面为抛物线形的隧道底部宽AB为12m,最大高度OP为6m,如图,车辆双向通行,规定车辆必须在中心线右侧,距道路边缘2m这一范围内行驶,并保持车辆顶部与隧道有不少于0.4m的空隙,现以AB中点O为原点,AB所在直线为x轴建立直角坐标系.分析 (1)设抛物线的函数关系式为y=ax2+6,找出函数图象上的坐标,求出函数解析式即可;
(2)根据题意,求出当x=6-2时y的值,根据车辆顶部与隧道的空隙不少于0.4米可得出不等式,从而得出通过隧道车辆的高度的最大值.
解答 解:(1)可设抛物线的函数关系式为y=ax2+6(a<0),
把点B(6,0)坐标代入上式,得0=36a+6,
解得:a=-$\frac{1}{6}$.
故y=-$\frac{1}{6}$x2+6(-6≤x≤6).
(2)如图,用线段EF表示通过隧道车辆的高度h米,延长FE交抛物线于点C,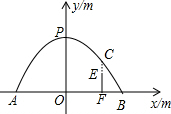
根据题意,则CE=CF-EF=-$\frac{1}{6}$x2+6-h≥0.4,
整理得:h≤-$\frac{1}{6}$x2+5.6(-4≤x≤4,且 x≠0 ).
∵a=-$\frac{1}{6}$<0,
∴当0<x≤4时,二次函数h随x的增大而减小;
当x=4时,函数h取得最小值,最小值为 h=-$\frac{1}{6}$×42+5.6≈2.93,
∴h≤2.93.
所以,通过隧道车辆的高度不能超过2.93米.
点评 本题考查了二次函数的应用,涉及了待定系数法求二次函数解析式得知识,解答本题的关键是建立直角坐标系,将实际问题转化为数学模型,难度一般.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校八年级3月月考数学试卷(解析版) 题型:解答题
根据国家发改委实施“阶梯电价”的有关文件要求,某市决定从2013年4月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:
一户居民一个月用电量的范围 | 电费价格(单位:元/千瓦时) |
不超过180千瓦时的部分 | a |
超过180千瓦时的部分 | b |
2013年5月份,该市居民甲用电100千瓦时,交电费60元;居民乙用电200千瓦时,交电费121元.
(1)上表中,a= ;b= ;(2)随着夏天的到来,用电量将增加.为了节省开支,该市居民小王计划把今年6月份的电费控制在不超过家庭月收入的2%.若小王家庭月收入为9300元,则小王家今年6月份最多能用电多少千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
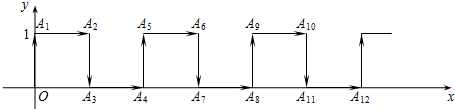
 如图,在直角坐标系中,设一动点M自P0(1,0)初向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x7=-1;以此类推,x1+x2+…+x2014+x2015=-1.
如图,在直角坐标系中,设一动点M自P0(1,0)初向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x7=-1;以此类推,x1+x2+…+x2014+x2015=-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
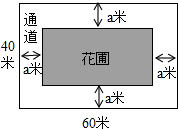 如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
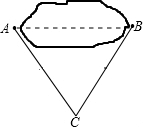 如图,小雪为了估计池塘边A,B两点的距离,他在池塘外取一点C,测得AC=7米,BC=5米,则A,B两点的距离可能为( )
如图,小雪为了估计池塘边A,B两点的距离,他在池塘外取一点C,测得AC=7米,BC=5米,则A,B两点的距离可能为( )| A. | 11米 | B. | 12米 | C. | 13米 | D. | 14米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com