
【题目】如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.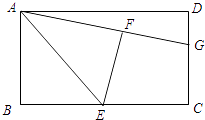
(1)猜想线段GF与GC有何数量关系?并证明你的结论;
(2)若AB=3,AD=4,求线段GC的长.
【答案】
(1)解:GF=GC.
理由如下:连接GE, 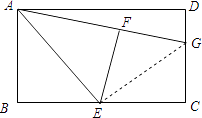
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=90°,
∴∠EFG=90°,
∵在Rt△GFE和Rt△GCE中,
![]() ,
,
∴Rt△GFE≌Rt△GCE(HL),
∴GF=GC;
(2)解:设GC=x,则AG=3+x,DG=3﹣x,
在Rt△ADG中,42+(3﹣x)2=(3+x)2,
解得x= ![]() .
.
【解析】(1) GF=GC,理由如下:连接GE, 由中点定义折叠的性质得出EF=EC,由矩形的性质得出∠C=90°,∠EFG=90°,从而利用HL证出Rt△GFE≌Rt△GCE,根据全等三角形对应边相等得出结论;
(2)设GC=x,则AG=3+x,DG=3﹣x,在Rt△ADG中根据勾股定理列出方程求解即可。


科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,E、F分别BC、AD边上,AE=BF,AE与BF交于G,ED与CF交于H.求证: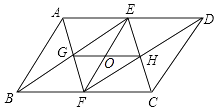
(1)GH∥BC;
(2)GH= ![]() AD.
AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,E,F,C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD.则当点E,F不重合时,BD与EF的关系是______.
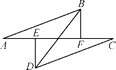
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,D是AB边的中点,E是AC边上一点,联结DE,过点D作
,D是AB边的中点,E是AC边上一点,联结DE,过点D作![]() 交BC边于点F,联结EF.
交BC边于点F,联结EF.
(1)如图1,当![]() 时,求EF的长;
时,求EF的长;
(2)如图2,当点E在AC边上移动时, ![]() 的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出
的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出![]() 的正切值;
的正切值;
(3)如图3,联结CD交EF于点Q,当![]() 是等腰三角形时,请直接写出BF的长.
是等腰三角形时,请直接写出BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.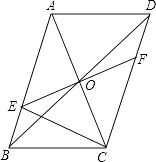
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,求ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。

证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com