
【题目】如图,已知平行四边形ABCD中,E、F分别BC、AD边上,AE=BF,AE与BF交于G,ED与CF交于H.求证: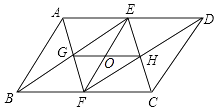
(1)GH∥BC;
(2)GH= ![]() AD.
AD.
【答案】
(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∵AE=BF,
∴四边形ABFE为平行四边形,
∵AD=BC,
∴DE=FC,
同理可得四边形CDEF为平行四边形,
∴G为AF的中点,H为DF的中点,
∴GH为△ADF的中位线,
∴GH∥AD,
∴GH∥BC;
(2)证明:∵GH为△ADF的中位线,
∴GH= ![]() AD.
AD.
【解析】(1)根据已知四边形ABCD为平行四边形,AE=BF,易证得四边形ABFE为平行四边形,四边形CDEF为平行四边形,根据平行四边形的性质得出GH为△ADF的中位线,即可证得结论。
(2)由(1)证明过程可知GH为△ADF的中位线,即可证得结论。
【考点精析】本题主要考查了三角形中位线定理和平行四边形的判定与性质的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知 ![]() ,在射线
,在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心的圆与
为圆心的圆与 ![]() 相切;在射线
相切;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切;在射线
相切;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切;
相切; ![]() ;在射线
;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切.若
相切.若 ![]() 的半径为
的半径为 ![]() ,则
,则 ![]() 的半径长是 .
的半径长是 . 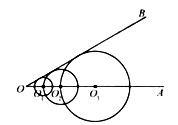
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从![]() 地匀速驶往相距350km的
地匀速驶往相距350km的![]() 地,当货车行驶1小时经过途中的
地,当货车行驶1小时经过途中的![]() 地时,一辆快递车恰好从
地时,一辆快递车恰好从![]() 地出发以另一速度匀速驶往
地出发以另一速度匀速驶往![]() 地,当快递车到达
地,当快递车到达![]() 地后立即掉头以原来的速度匀速驶往
地后立即掉头以原来的速度匀速驶往![]() 地.(货车到达
地.(货车到达![]() 地,快递车到达
地,快递车到达![]() 地后分别停止运动)行驶过程中两车与
地后分别停止运动)行驶过程中两车与![]() 地间的距离
地间的距离![]() (单位:
(单位:![]() )与货车从出发所用的时间
)与货车从出发所用的时间![]() (单位:
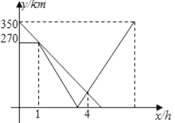
(单位:![]() )间的关系如图所示.则货车到达
)间的关系如图所示.则货车到达![]() 地后,快递车再行驶______
地后,快递车再行驶______![]() 到达
到达![]() 地.
地.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学要证明命题“平行四边形的对边相等.”是正确的,他画出了图形,并写出了如下已知和不完整的求证.
已知:如图,四边形ABCD是平行四边形.
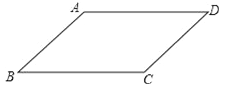
求证:AB=CD,
(1)补全求证部分;
(2)请你写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个转盘,转盘被分成4个相同的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),求下列事件的概率:
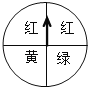
(1)指针指向绿色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABOC的顶点O在坐标原点,顶点B,C分别在x,y轴的正半轴上,顶点A在反比例函数y= ![]() (k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针反向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则
(k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针反向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则 ![]() 的值是 .
的值是 . 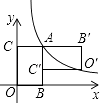
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.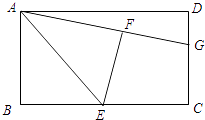
(1)猜想线段GF与GC有何数量关系?并证明你的结论;
(2)若AB=3,AD=4,求线段GC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com