
【题目】正方形ABCD中,AB=2,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 .
【答案】![]()
【解析】解:连接DE,交AC于点P,连接BD. 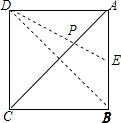
∵点B与点D关于AC对称,
∴DE的长即为PE+PB的最小值,
∵AB=2,E是BC的中点,
∴AE=1,
在Rt△CDE中,
DE= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用勾股定理的概念和正方形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,求证∠1=∠2.以下是推理过程,请你填空:
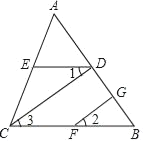
解:∵CD⊥AB,FG⊥AB
∴∠CDB=∠FGB=90°( 垂直定义)
∴ ∥FG( )
∴ =∠3 ( )
又∵DE∥BC ( 已知 )
∴∠ =∠3 ( 两直线平行,内错角相等 )
∴∠1=∠2 ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线 y=x+2 与两坐标轴分别交于A、B 两点,点 C 是 OB 的中点,D、E 分 别是直线 AB、y 轴上的动点,则△CDE 周长的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有个.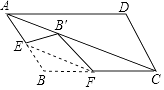
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() (x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=
(x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE= ![]() CB,AF=
CB,AF= ![]() AB,且四边形OEBF的面积为2,则k的值为 .
AB,且四边形OEBF的面积为2,则k的值为 . 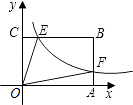
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,E、F分别BC、AD边上,AE=BF,AE与BF交于G,ED与CF交于H.求证: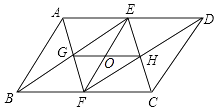
(1)GH∥BC;
(2)GH= ![]() AD.
AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,E,F,C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD.则当点E,F不重合时,BD与EF的关系是______.
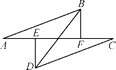
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com