
【题目】如图,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,求证∠1=∠2.以下是推理过程,请你填空:
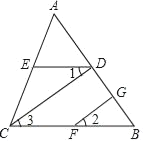
解:∵CD⊥AB,FG⊥AB
∴∠CDB=∠FGB=90°( 垂直定义)
∴ ∥FG( )
∴ =∠3 ( )
又∵DE∥BC ( 已知 )
∴∠ =∠3 ( 两直线平行,内错角相等 )
∴∠1=∠2 ( )
科目:初中数学 来源: 题型:
【题目】将一副直角三角板如图摆放,等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,BC= ![]() .以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则
.以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则 ![]() 的长为 ( )
的长为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 ![]() ,在射线
,在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心的圆与
为圆心的圆与 ![]() 相切;在射线
相切;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切;在射线
相切;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切;
相切; ![]() ;在射线
;在射线 ![]() 上取点
上取点 ![]() ,以
,以 ![]() 为圆心,
为圆心, ![]() 为半径的圆与
为半径的圆与 ![]() 相切.若
相切.若 ![]() 的半径为
的半径为 ![]() ,则
,则 ![]() 的半径长是 .
的半径长是 . 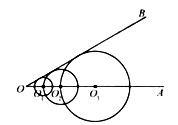
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.附图(①)为一张三角形ABC纸片,P点在BC上.今将A折至P时,出现折线BD,其中D点在AC上,如图(②)所示.若△ABC的面积为80,△DBC的面积为50,则BP与PC的长度比为何?( )
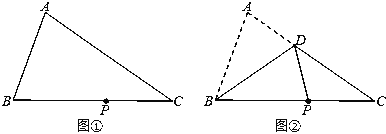
A.3:2 B.5:3 C.8:5 D.13:8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
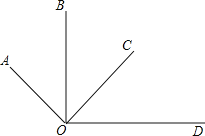
①∠AOB=∠COD;
②∠AOB+∠COD=90°;
③∠BOC+∠AOD=180°;
④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABOC的顶点O在坐标原点,顶点B,C分别在x,y轴的正半轴上,顶点A在反比例函数y= ![]() (k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针反向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则
(k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针反向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则 ![]() 的值是 .
的值是 . 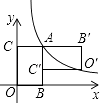
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com