【题目】如图，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（ ）
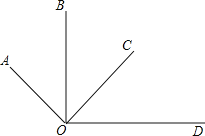
①∠AOB=∠COD；
②∠AOB+∠COD=90°；
③∠BOC+∠AOD=180°；
④∠AOC-∠COD=∠BOC．
A．①②③
B．①②④
C．①③④
D．②③④
七彩题卡口算应用一点通系列答案科目：初中数学 来源： 题型：
【题目】先阅读下面例题的解法，然后解答问题：
例：若多项式2x3-x2+m分解因式的结果中有因式2x+1，求实数m的值.
解：设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0，则2x+1=0或A=0.
由2x+1=0，解得x=-
.
∴x=-是方程2x3-x2+m=0的解. ∴2×(-)3-(-)2+m=0，即-
-+m=0. ∴m=.
(1)若多项式x2+px-6分解因式的结果中有因式x-3，则实数p= ；
(2)若多项式x3+5x2+7x+q分解因式的结果中有因式x+1，求实数q的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点B、E分别在直线AC和DF上，若∠AGB=∠EHF，∠C=∠D，可以证明∠A=∠F．请完成下面证明过程中的各项“填空”．
证明：∵∠AGB=∠EHF（理由： ）
∠AGB= （对顶角相等）
∴∠EHF=∠DGF，∴DB∥EC（理由： ）
∴ =∠DBA（两直线平行，同位角相等）
又∵∠C=∠D，∴∠DBA=∠D，
∴DF∥ （内错角相等，两直线平行）
∴∠A=∠F（理由： ）．
查看答案和解析>>
科目：初中数学 来源： 题型：
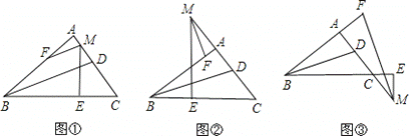
【题目】小明在学习三角形知识时，发现如下三个有趣的结论：在Rt△ABC中，∠A＝90°，BD平分∠ABC，M为直线AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线AB于点F．
（1）如图①，M为边AC上一点，则BD、MF的位置关系是 ；
如图②，M为边AC反向延长线上一点，则BD、MF的位置关系是 ；
如图③，M为边AC延长线上一点，则BD、MF的位置关系是 ；
（2）请就图①、图②、或图③中的一种情况，给出证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
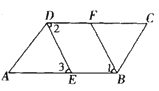
【题目】已知：如图，DE∥AB．请根据已知条件进行推理，分别得出结论，并在括号内注明理由．
（1）∵DE∥AB，（ 已知 ）
∴∠2= ． （ ， ）
（2）∵DE∥AB，（已知 ）
∴∠3= ．（ ， ）
（3）∵DE∥AB（已知 ），
∴∠1+ =180°．（ ， ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，∠ABC＝∠ADC，BF、DE分别平分∠ABC与∠ADC．∠1＝∠3，求证：AB∥DC．
证明：∵∠ABC＝∠ADC ( )
∴
( )
∵BF、DE分别平分∠ABC与∠ADC ( )
∴
( )
∴∠______＝∠______ ( )
∵∠1＝∠3( )
∴∠2＝∠______ (等量代换)
∴____∥____ ( )
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店用1000元购进一批套尺，很快销售一空；商店又用1500元购进第二批同款套尺，购进单价比第一批贵25%，所购数量比第一批多100套.
（1）求第一批套尺购进的单价；
（2）若商店以每套4元的价格将这两批套尺全部售出，可以盈利多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
