
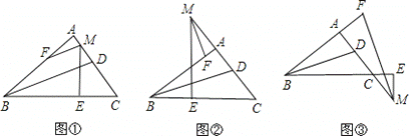
����Ŀ��С����ѧϰ������֪ʶʱ����������������Ȥ�Ľ��ۣ���Rt��ABC�У���A��90�㣬BDƽ�֡�ABC��MΪֱ��AC��һ�㣬ME��BC������ΪE����AME��ƽ���߽�ֱ��AB�ڵ�F��
��1����ͼ�٣�MΪ��AC��һ�㣬��BD��MF��λ�ù�ϵ�� ��
��ͼ�ڣ�MΪ��AC�����ӳ�����һ�㣬��BD��MF��λ�ù�ϵ�� ��
��ͼ�ۣ�MΪ��AC�ӳ�����һ�㣬��BD��MF��λ�ù�ϵ�� ��
��2�����ͼ�١�ͼ�ڡ���ͼ���е�һ�����������֤��.
���𰸡���1��BD��MF��BD��MF��BD��MF����2��֤����������
��������
���⣨1��ƽ�У���ֱ����ֱ�� 3��
��2��ѡ�� ֤��BD��MF
�������£��ߡ�A=90����ME��BC��
���ABC+��AME=360�㩁90���2=180���� 1��
��BDƽ����ABC��MFƽ����AME��
���ABD=![]() ��ABC����AMF=
��ABC����AMF=![]() ��AME��
��AME��
���ABD+��AMF=![]() ����ABC+��AME��=90���� 2��
����ABC+��AME��=90���� 2��
���ߡ�AFM+��AMF=90����
���ABD=��AFM�� 3��
��BD��MF�� 4��
ѡ�� ֤��BD��MF��
�������£��ߡ�A=90����ME��BC��
���ABC+��C=��AME+��C=90����
���ABC=��AME�� 1��
��BDƽ����ABC��MFƽ����AME��
���ABD=��AMF�� 2��
�ߡ�ABD+��ADB=90����
���AMF+��ADB=90���� 3��
��BD��MF�� 4��
ѡ�� ֤��BD��MF��
�������£��ߡ�A=90����ME��BC��
���ABC+��ACB=��AME+��ACB=90����
���ABC=��AME�� 1��
��BDƽ����ABC��MFƽ����AME��
���ABD=��AMF�� 2��
�ߡ�AMF+��F=90����
���ABD+��F=90���� 3��
��BD��MF�� 4��


 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
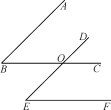
����Ŀ����ͼ����֪BC��DE�ཻ�ڵ�O���������������жϣ���AB��DE����BC��EF���ۡ�B����E�����������������ж���Ϊ���裬����һ���ж���Ϊ���ۣ�д�����е����⣬ָ����Щ������������Ǽ����⣬��ѡ�����е�һ�����������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��Ѱ����Ϸ��Ѱ��ͨ����ͼ1��ʾ��ͨ������ͬһƽ���ڵ�AB��BC��CA��OA��OB��OC��ɣ�Ϊ��¼Ѱ���ߵ��н�·�ߣ���BC���е�M��������һ̨��λ��������Ѱ�����н���ʱ��Ϊx��Ѱ�����붨λ����֮��ľ���Ϊy����Ѱ���������н����ұ�ʾy��x�ĺ�����ϵ��ͼ�������ͼ2��ʾ����Ѱ���ߵ��н�·�߿���Ϊ�� ��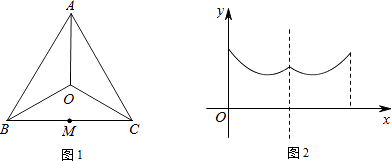
A.A��O��B
B.B��A��C
C.B��O��C
D.C��B��O
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������жϴ�����ǣ� ��

A. �����2=��4����ôAB��CD B. �����1=��3����ôAB��CD
C. �����BAD+��D=180�㣬��ôAB��CD D. �����BAD+��B=180����ôAD��CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��Ϊ����ʡ�����������У��ƻ������е�·���Ե����е����и��죬�������֪�����ù����ɼ��̶ӵ�������ǡ���ڹ涨ʱ������ɣ����ù������ҹ��̶ӵ�����ɣ�����Ҫ�������ǹ涨ʱ���2�������ס��������̶Ӻ���6������µĹ����ɼ��̶ӵ�����������3����ɣ�
��1���ʸ���Ҫ���������̹涨��ʱ���Ƕ����죿
��2����֪���̶���һ���踶������5��Ԫ���ҹ��̶���һ���踶������3��Ԫ���ָù����ɼס����������̶Ӻ�����ɣ��������˹��̹��ʿ�65��Ԫ�����ʸ������Ĺ��̹��ʿ��Ƿ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA��OC��OB��OD����������У�����˵����ȷ���ǣ�������
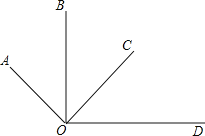
�١�AOB=��COD��
�ڡ�AOB+��COD=90�㣻
�ۡ�BOC+��AOD=180�㣻
�ܡ�AOC-��COD=��BOC��
A���٢ڢ�
B���٢ڢ�
C���٢ۢ�
D���ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijСѧΪ���˽���꼶���ض�ͯ����������һ�����꼶���ض�ͯ����������ͳ�ƣ��õ�ÿ���꼶�����ض�ͯ�����ֱ�Ϊ10��15��10��17��18��20�������������ݣ�����˵��������ǣ� ��
A.ƽ������15
B.������10
C.�����17
D.������ ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��EF�����A����C����D����E�����������ϵ�ǣ� ��

A. ��A����C����D����E��360��
B. ��A����D����C����E
C. ��A����C����D����E��180��
D. ��E����C����D����A��90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
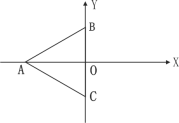
����Ŀ����ͼ���ȱ�������ABC�Ķ���B��0��2����A��x�Ḻ��������C��y�Ḻ������.
��1��д��A��C��������ꣻ
��2������ABC��������ܳ�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com