
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.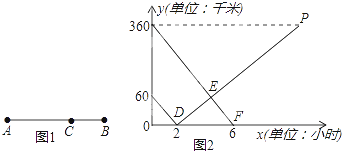
(1)填空:A,B两地相距千米;货车的速度是千米/时.
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数表达式;
(3)客、货两车何时相遇?
【答案】
(1)420,30
(2)解:设2小时后,货车离C站的路程y2与行驶时间x之间的函数表达式为y2=kx+b,根据题意得
360÷30=12(h),12+2=14(h)
∴点P的坐标为(14,360)
将点D(2,0)、点P(14,360)代入y2=kx+b中, ![]()
解得 k=30,b=﹣60
∴y2=30x﹣60
(3)解:设客车离C站的路程y1与行驶时间x之间的函数表达式为y1=k1x+b1,
根据题意得
![]()
解得k1=﹣60,b1=360
y1=﹣60x+360
由y1=y2得
30x﹣60=﹣60x+360
解得x= ![]()
答:客、货两车在出发后 ![]() 小时相遇.
小时相遇.
【解析】根据时间为0时,客车和货车距离C站的距离即可解题,图中给的函数图像和题意可以直接得到A、B两地的距离。
(2)根据题意和函数图像中的数据可以得出两个小时后,货车离C站的路程y2与行驶时间x之间的函数关系式,一般求解函数解析式,利用待定系数法进行求解。
(3)两个函数图像相交,说明两辆车相遇。根据图中的数据分析,利用待定系数法,可求得客车离C站的路程y1与行驶时间x之间的函数解析式,然后令y1=y2,联立得方程,即解得两辆车相遇


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
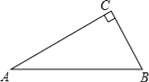
【题目】如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)
(2)连接BD,求证:DE=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AOBC,点A、B分别在x、y轴上,对角线AB、OC交于点D,点C( ![]() ,1),点M是射线OC上一动点.
,1),点M是射线OC上一动点.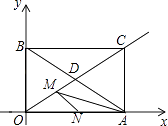
(1)求证:△ACD是等边三角形;
(2)若△OAM是等腰三角形,求点M的坐标;
(3)若N是OA上的动点,则MA+MN是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小莉的爸爸买了某演唱会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,5的四张牌给小莉,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)请用树状图或列表的方法表示出两张牌数字相加和的所有可能出现的结果;
(2)哥哥设计的游戏规则公平吗?为什么?若不公平,请设计一种公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答问题.
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴![]() ,∴a=2,b=1
,∴a=2,b=1
∴![]() =
=![]() =
=![]() +
+![]() =x2+2+
=x2+2+![]() 这样,分式
这样,分式![]() 被拆分成了一个整式x2+2与一个分式
被拆分成了一个整式x2+2与一个分式![]() 的和.
的和.
解答:
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)试说明![]() 的最小值为8.
的最小值为8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时)。
(1)用有序实数对表示图中各点。
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com