
【题目】阅读理解
在平面直角坐标系xoy中,两条直线l1:y=k1x+b1(k1≠0),l2:y=k2x+b2(k2≠0),①当l1∥l2时,k1=k2,且b1≠b2;②当l1⊥l2时,k1·k2=-1.
类比应用
(1)已知直线l:y=2x-1,若直线l1:y=k1x+b1与直线l平行,且经过点A(-2,1),试求直线l1的表达式;
拓展提升
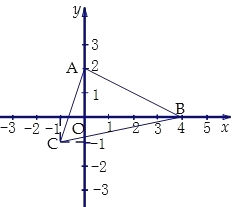
(2)如图,在平面直角坐标系xoy中,△ABC的顶点坐标分别为:A(0,2),B(4,0),C(-1,-1),试求出AB边上的高CD所在直线的表达式.
【答案】(1)y=2x+5;(2)y=2x+1.
【解析】
(1)利用平行线性质可知k值相等,进而将P点坐标代入l1即可求出直线l1的表达式;
(2)由题意设直线AB的表达式为:y=kx+b,求出直线AB的表达式,再根据题意设AB边上的高CD所在直线的表达式为:y=mx+n,进行分析求出CD所在直线的表达式.
解:(1)∵l1∥l,
∴k1=2,
∵直线经过点P(-2,1),
∴1=2×(-2)+b1,b1=5,
∴直线l1表达式为:y=2x+5.
(2)设直线AB的表达式为:y=kx+b
∵直线经过点A(0,2),B(4,0),
∴![]() , 解得:
, 解得: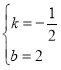 ,
,
∴直线AB的表达式为:![]() ;
;
设AB边上的高CD所在直线的表达式为:y=mx+n,
∵CD⊥AB,
∴m·(![]() )=-1,m=2,
)=-1,m=2,
∵直线CD经过点C(-1,-1),
∴-1=2×(-1)+n,n=1,
∴AB边上的高CD所在直线的表达式为:y=2x+1.


科目:初中数学 来源: 题型:
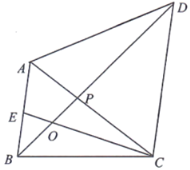
【题目】如图,四边形ABCD中,![]() ,
,![]() ,
,![]() ,对角线BD平分
,对角线BD平分![]() 交AC于点P.CE是
交AC于点P.CE是![]() 的角平分线,交BD于点O.
的角平分线,交BD于点O.
(1)请求出![]() 的度数;
的度数;
(2)试用等式表示线段BE、BC、CP之间的数量关系,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.
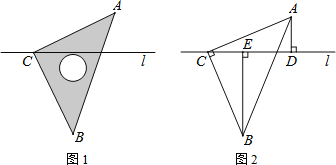
(1)△ACD与△CBE全等吗?说明你的理由.
(2)猜想线段AD、BE、DE之间的关系.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
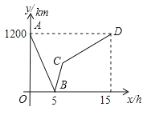
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,慢车的速度是快车速度的![]() ,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
根据图象解决以下问题:
(1)甲、乙两地之间的距离为 km;D点的坐标为 ;
(2)求线段BC的函数关系式,并写出自变量x的取值范围;
(3)若第二列快车从乙地出发驶往甲地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车追上慢车.求第二列快车比第一列快车晚出发多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④APAD=CQCB.其中正确的是( )
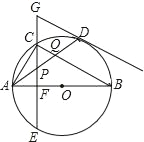
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3000元购进某种干果销售,由于销售状况良好,很快售完.超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果的数量是第一次的2倍还多300千克,如果超市此时按每千克9元的价格出售,当大部分干果售出后,余下的100千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市第二次销售该种干果盈利了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
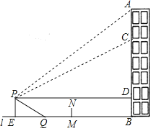
【题目】如图,重庆某广场新建与建筑物![]() 垂直的空中玻璃走廊
垂直的空中玻璃走廊![]() 与
与![]() 相连,
相连,![]() 与地面
与地面![]() 垂直.在
垂直.在![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() ,测得建筑物
,测得建筑物![]() 处的仰角为
处的仰角为![]() (不计测量人员的身高),
(不计测量人员的身高),![]() 为
为![]() 米.图中的点
米.图中的点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 及直线
及直线![]() 均在同一平面内.
均在同一平面内.
![]() 求
求![]() 、
、![]() 两点的高度差(结果精确到
两点的高度差(结果精确到![]() 米);
米);
![]() 为方便游客,广场从地面
为方便游客,广场从地面![]() 上的
上的![]() 点新建扶梯
点新建扶梯![]() ,
,![]() 所在斜面的坡度
所在斜面的坡度![]() ,
,![]() 到地面
到地面![]() 的距离
的距离![]() 为
为![]() 米.一广告牌
米.一广告牌![]() 位于
位于![]() 的中点
的中点![]() 处,市政规划要求在点
处,市政规划要求在点![]() 右侧需留出
右侧需留出![]() 米的行车道,请判断是否需要挪走广告牌
米的行车道,请判断是否需要挪走广告牌![]() ,并说明理由.(参考数据:
,并说明理由.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com