
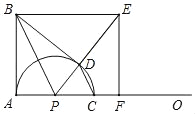
【题目】如图,∠BAO=90°,AB=8,动点P在射线AO上,以PA为半径的半圆P交射线AO于另一点C,CD∥BP交半圆P于另一点D,BE∥AO交射线PD于点E,EF⊥AO于点F,连接BD,设AP=m.
(1)求证:∠BDP=90°.
(2)若m=4,求BE的长.
(3)在点P的整个运动过程中.
①当AF=3CF时,求出所有符合条件的m的值.
②当tan∠DBE=![]() 时,直接写出△CDP与△BDP面积比.
时,直接写出△CDP与△BDP面积比.
【答案】(1)详见解析;(2)![]() 的长为10;(3)m的值为
的长为10;(3)m的值为![]() 或
或![]() ;
;![]() 与
与![]() 面积比为
面积比为![]() 或
或![]() .
.
【解析】
![]() 由
由![]() 知
知![]() ,再由
,再由![]() 知
知![]() 、
、![]() ,据此可得
,据此可得![]() ,证
,证![]() ≌
≌![]() 即可得;
即可得;![]() 易知四边形ABEF是矩形,设
易知四边形ABEF是矩形,设![]() ,可得
,可得![]() ,证
,证![]() ≌
≌![]() 得
得![]() ,在
,在![]() 中,由
中,由![]() ,列方程求解可得答案;
,列方程求解可得答案;![]() 分点C在AF的左侧和右侧两种情况求解:左侧时由
分点C在AF的左侧和右侧两种情况求解:左侧时由![]() 知
知![]() 、
、![]() 、
、![]() ,在
,在![]() 中,由
中,由![]() 可得关于m的方程,解之可得;右侧时,由
可得关于m的方程,解之可得;右侧时,由![]() 知
知![]() 、
、![]() 、
、![]() ,利用勾股定理求解可得.
,利用勾股定理求解可得.![]() 作
作![]() 于点G,延长GD交BE于点H,由
于点G,延长GD交BE于点H,由![]() ≌
≌![]() 知
知![]() ,据此可得
,据此可得 ,再分点D在矩形内部和外部的情况求解可得.
,再分点D在矩形内部和外部的情况求解可得.
![]() 如图1,
如图1,

![]() ,
,
![]() ,
,
![]() ,
,
![]() 、
、![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形ABEF是矩形,
四边形ABEF是矩形,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
解得:![]() ,
,
![]() 的长为10.
的长为10.
![]() 如图1,当点C在AF的左侧时,
如图1,当点C在AF的左侧时,
![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,由
中,由![]() 可得
可得![]() ,
,
解得:![]() 负值舍去
负值舍去![]() ;
;
如图2,当点C在AF的右侧时,

![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,由
中,由![]() 可得
可得![]() ,
,
解得:![]() 负值舍去
负值舍去![]() ;
;
综上,m的值为![]() 或
或![]() ;
;
![]() 如图3,过点D作
如图3,过点D作![]() 于点G,延长GD交BE于点H,
于点G,延长GD交BE于点H,

![]() ≌
≌![]() ,
,
![]() ,
,
又![]() ,且
,且![]() ,
,
 ,
,
当点D在矩形ABEF的内部时,
由![]() 可设
可设![]() 、
、![]() ,
,
则![]() ,
,
![]() ,
,
则![]() ;
;
如图4,当点D在矩形ABEF的外部时,

由![]() 可设
可设![]() 、
、![]() ,
,
则![]() ,
,
![]() ,
,
则![]() ,
,
综上,![]() 与
与![]() 面积比为
面积比为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】因商人、商业、商品发源于商丘,商朝建都于河南商丘,商丘被誉为“三商之源,华商之都”![]() 商字是商丘市的城市地标,坐落在河南省商丘市睢阳区神火大道与南京路交汇处中的环岛内,雕塑建成与1997年6月29日,某中学九年级数学兴趣小组想测量商字雕塑AB的高度,小明在雕塑前一座写字楼CD分E处仰望商字雕塑的顶端A,测得仰角为
商字是商丘市的城市地标,坐落在河南省商丘市睢阳区神火大道与南京路交汇处中的环岛内,雕塑建成与1997年6月29日,某中学九年级数学兴趣小组想测量商字雕塑AB的高度,小明在雕塑前一座写字楼CD分E处仰望商字雕塑的顶端A,测得仰角为![]() ,小亮在写字楼前F处,测得商字雕塑的顶端A的仰角为
,小亮在写字楼前F处,测得商字雕塑的顶端A的仰角为![]() ,有装B,F,D在同一条直线上,
,有装B,F,D在同一条直线上,![]() ,
,![]() ,求商字雕塑AB的高度
,求商字雕塑AB的高度![]() 测角器的高度忽略不计,结果精确到1米
测角器的高度忽略不计,结果精确到1米![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD和正方形EFGH的中心重合,![]() ,
,![]() ,
,![]() 分别延长FE,GF,HG和EH交AB,BC,CD,AD于点I,J,K,
分别延长FE,GF,HG和EH交AB,BC,CD,AD于点I,J,K,![]() 若
若![]() ,则AI的长为______,四边形AIEL的面积为______.
,则AI的长为______,四边形AIEL的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数![]() 和y=x的图象于点C,D.
和y=x的图象于点C,D.
(1)求点A的坐标;
(2)若OB=CD,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式,![]()
解:∵![]() ,∴
,∴![]() 可化为,
可化为,![]()
由有理数的乘法法则“两数相乘,同号得正”,有
(1)![]() 或(2)
或(2)![]()
解不等式组(1),得![]() ,解不等式组(2),得
,解不等式组(2),得![]() ,
,
故![]() 的解集为
的解集为![]() 或
或![]() ,
,
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
问题:(1)一元二次不等式![]() 的解集为______.
的解集为______.
(2)求分式不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在学习“实数”时画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交数轴于点A”,请根据图形回答下列问题:
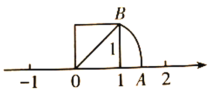
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式体现了 的数学思想方法.(将下列符合的选项序号填在横线上)
A.数形结合 B.代入 C.换元 D.归纳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com