
【题目】小刚在A,B两家体育用品商店都发现了他看中的羽毛球拍和篮球,两家商店的羽毛球拍和篮球的单价都是相同的,羽毛球拍和篮球单价之和是426元,且篮球的单价是羽毛球拍的单价的4倍少9元.
(1)求小刚看中的羽毛球拍和篮球的单价各是多少元?
(2)小刚在元旦这一天上街,恰好赶上商店促销,A商店所有商品打八五折销售,B商店全场购物满100元返购物券20元(不足100元不返券,购物券全场通用,用购物券购物不再返券),但他只带了380元钱,如果他只在一家商店购买看中的这两样商品,你能说明他可以选择在哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
【答案】
(1)解:设羽毛球拍单价为x元,则篮球的单价是(4x﹣9)元,
依题意得:x+4x﹣9=426,
解得x=87,
则426﹣87=339.
答:羽毛球拍单价为87元,则篮球的单价是339元
(2)解:在A商场购物更省钱;
理由:∵A商场所有商品打八五折销售,
∴A商场所付金额为:426×0.85=362.1(元),
∵B商场全场满100元返购物卷20元(不足100元不反卷,购物卷全场通用),
∴先购买篮球339元,赠购物卷60元,
故此次只需要339+27=366(元),
故在A商场购物更省钱
【解析】(1)将题中关键的已知条件转化为相等关系:羽毛球拍的单价+篮球单价=426元,篮球的单价=羽毛球拍的单价![]() 4-9,设未知数,建立方程求解即可。
4-9,设未知数,建立方程求解即可。
(2)抓住关键的已知条件:两家商店的羽毛球拍和篮球的单价都是相同的,先根据题意分别求出A、B商场所付的金额,再比较大小即可得出结论。
【考点精析】掌握解一元一次方程的步骤是解答本题的根本,需要知道先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了.


科目:初中数学 来源: 题型:
【题目】如图是一个正方体盒子的表面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字互为相反数.
(1)把﹣16,9,16,﹣5,﹣9,5分别填入图中的六个小正方形中;
(2)若某相对两个面上的数字分别为 ![]() 和
和 ![]() ﹣5,求x的值.
﹣5,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级进行法律知识竞赛,共有30道题,答对一道题得4分,不答或答错一道题扣2分.
(1)小红同学参加了竞赛,成绩是90分,请问小红在竞赛中答对了多少道题?
(2)小明也参加了竞赛,考完后他说:“这次竞赛我一定能拿到100分.”请问小明有没有可能拿到100分?试用方程的知识来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=( ) 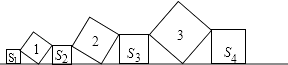
A.5
B.4
C.6
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.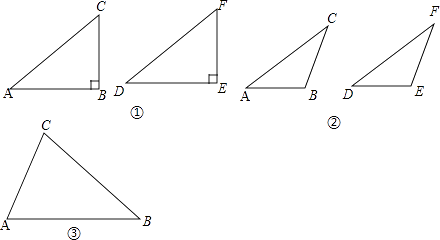
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 , 可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若 , 则△ABC≌△DEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com