
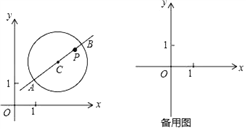
【题目】在平面直角坐标系xOy中,⊙C的半径为r(r>1),P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:若直线CP与⊙C交于点A,B,满足|PA-PB|=2,则称点P为⊙C的“完美点”,如图为⊙C及其“完美点”P的示意图.
(1)当⊙O的半径为2时,
①点M(![]() ,0) ⊙O的“完美点”,点N(0,1) ⊙O的“完美点”,点T(-
,0) ⊙O的“完美点”,点N(0,1) ⊙O的“完美点”,点T(-![]() ,-
,- ![]() ) ⊙O的“完美点”(填“是”或者“不是”);
) ⊙O的“完美点”(填“是”或者“不是”);
②若⊙O的“完美点”P在直线y=![]() x上,求PO的长及点P的坐标;
x上,求PO的长及点P的坐标;
(2)⊙C的圆心在直线y=![]() x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
【答案】(1)①点M不是⊙O的“完美点”,点N是⊙O的“完美点”.点T是⊙O的“完美点”.
②OP=1,点P的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).(2)1
).(2)1![]() ≤t≤1+
≤t≤1+![]() .
.
【解析】解:(1)点M不是⊙O的“完美点”,
点N是⊙O的“完美点”.
点T是⊙O的“完美点”.
②根据题意,|PA![]() PB|=2,
PB|=2,
∴|OP+2![]() (2
(2![]() OP)|=2∴OP=1.
OP)|=2∴OP=1.
若点P在第一象限内,作PQ⊥x轴于点Q,∵点P在直线![]() 上,OP=1,
上,OP=1,
∴OQ=![]() ,PQ=
,PQ=![]() .∴P(
.∴P(![]() ,
, ![]() ).
).
若点P在第三象限内,根据对称性可知其坐标为(![]()
![]() ,
, ![]()
![]() ).
).
综上所述,PO的长为1,点P的坐标为(![]() ,
, ![]() )或(
)或(![]()
![]() ,
, ![]()
![]() ).
).
(2)对于⊙C的任意一个“完美点”P都有|PA﹣PB|=2,
∴|CP+2![]() (2
(2![]() CP)|=2.∴CP=1.
CP)|=2.∴CP=1.
∴对于任意的点P,满足CP=1,都有|CP+2![]() (2
(2![]() CP)|=2,
CP)|=2,
∴|PA﹣PB|=2,故此时点P为⊙C的“完美点”.因此,⊙C的“完美点”是以点C为圆心,1为半径的圆.
设直线![]() 与y轴交于点D,当⊙C移动到与y轴相切且切点在点D的下方时,t的值最小.
与y轴交于点D,当⊙C移动到与y轴相切且切点在点D的下方时,t的值最小.
设切点为E,连接CE,∵⊙C的圆心在直线y=![]() x+1上,∴此直线和x轴,y轴的交点C(0,1),F(﹣
x+1上,∴此直线和x轴,y轴的交点C(0,1),F(﹣![]() ,0),∴OF=
,0),∴OF=![]() ,OD=1,∵CE∥OF,∴△DOF∽△DEC,∴
,OD=1,∵CE∥OF,∴△DOF∽△DEC,∴![]() ,∴
,∴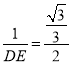 ,∴DE=
,∴DE=![]() .t的最小值为1
.t的最小值为1![]()
![]() .当⊙C移动到与y轴相切且切点在点D的上方时,t的值最大.
.当⊙C移动到与y轴相切且切点在点D的上方时,t的值最大.
同理可得t的最大值为1+![]() .综上所述,t的取值范围为1
.综上所述,t的取值范围为1![]()
![]() ≤t≤1+
≤t≤1+![]()


科目:初中数学 来源: 题型:
【题目】下列计算中,正确的是( )
A. 6a+4b=10abB. 7x2y﹣3x2y=4x4y2
C. 7a2b﹣7ba2=0D. 8x2+8x2=16x4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
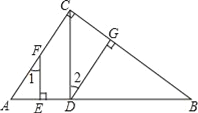
证明:∵DG⊥BC,AC⊥BC,(已知)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠DCA(等量代换)
∴EF∥CD( )
∴∠AEF=∠ADC( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°(等量代换)
∴CD⊥AB(垂直定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李家装修,客厅共需某种型号的地砖100块,经市场调查发现,如果购买彩色地砖40块和单色地砖60块则共需花费5600元,如果购买彩色地砖和单色地砖各50块,则需花费6000元.
(1)求两种型号的地砖的单价各是多少元/块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且购买地砖的费用不超过3400元,那么彩色地砖最多能采购多少决?
查看答案和解析>>
科目:初中数学 来源: 题型:
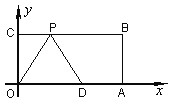
【题目】如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘西自治州风景优美,物产丰富,一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产.若购买3盒豆腐乳和2盒猕猴桃果汁共需180元;购买1盒豆腐乳和3盒猕猴桃果汁共需165元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com