
【题目】已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
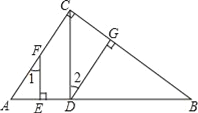
证明:∵DG⊥BC,AC⊥BC,(已知)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠DCA(等量代换)
∴EF∥CD( )
∴∠AEF=∠ADC( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°(等量代换)
∴CD⊥AB(垂直定义)
【答案】同位角相等,两直线平行;∠ACD; 两直线平行,内错角相等;同位角相等,两直线平行;两直线平行,同位角相等;垂直定义.
【解析】试题分析:已知DG⊥BC,AC⊥BC,根据垂直于同一条直线的两直线平行可得DG∥AC,由两直线平行,内错角相等可得∠2=∠ACD,已知∠1=∠2,等量代换得∠1=∠DCA,由同位角相等,两直线平行可得EF∥CD,由两直线平行,同位角相等可得∠AEF=∠ADC,已知EF⊥AB,由垂直定义可得∠AEF=90°,等量代换得∠ADC=90°,由垂直定义得CD⊥AB.
试题解析:
证明:∵DG⊥BC,AC⊥BC(已知),
∴DG∥AC(垂直于同一条直线的两直线平行 ),
∴∠2=∠ACD ( 两直线平行,内错角相等 ),
∵∠1=∠2(已知),
∴∠1=∠DCA(等量代换),
∴EF∥CD(同位角相等,两直线平行),
∴∠AEF=∠ADC(两直线平行,同位角相等),
∵EF⊥AB(已知),
∴∠AEF=90°(垂直定义),
∴∠ADC=90°(等量代换),
∴CD⊥AB(垂直定义).


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】在同一时刻,两根长度不等的竿子置于阳光之下,而它们的影长相等,那么这两根竿子的相对位置是( )
A. 两根都垂直于地面B. 两根平行斜插在地上C. 两根不平行D. 两根平行倒在地上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,结合题意写出当x取何值时,商场获利润不少于2160元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r(r>1),P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:若直线CP与⊙C交于点A,B,满足|PA-PB|=2,则称点P为⊙C的“完美点”,如图为⊙C及其“完美点”P的示意图.
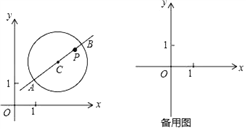
(1)当⊙O的半径为2时,
①点M(![]() ,0) ⊙O的“完美点”,点N(0,1) ⊙O的“完美点”,点T(-
,0) ⊙O的“完美点”,点N(0,1) ⊙O的“完美点”,点T(-![]() ,-
,- ![]() ) ⊙O的“完美点”(填“是”或者“不是”);
) ⊙O的“完美点”(填“是”或者“不是”);
②若⊙O的“完美点”P在直线y=![]() x上,求PO的长及点P的坐标;
x上,求PO的长及点P的坐标;
(2)⊙C的圆心在直线y=![]() x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
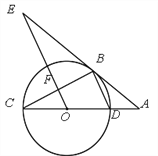
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A, ![]() ,OE交BC于点F.
,OE交BC于点F.
(1)求证:OE∥BD;
(2)当⊙O的半径为5, ![]() 时,求EF的长.
时,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com