
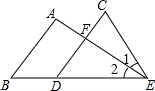
 已知,如图,AB∥CD,∠A=95°,∠C=65°,∠1:∠2=3:4,求∠B的度数.
已知,如图,AB∥CD,∠A=95°,∠C=65°,∠1:∠2=3:4,求∠B的度数.  同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:解答题
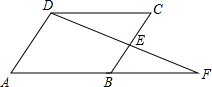 如图,在菱形ABCD中,点E是BC的中点,连接DE并延长与AB的延长线交于点F.
如图,在菱形ABCD中,点E是BC的中点,连接DE并延长与AB的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
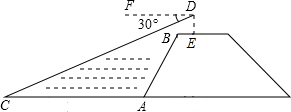 如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:$\sqrt{3}$≈1.73)
如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
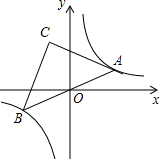 如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{8}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )| A. | y=$\frac{8}{x}$ | B. | y=$\frac{16}{x}$ | C. | y=-$\frac{16}{x}$ | D. | y=-$\frac{8}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x+2 | B. | y=2x+1 | C. | y=2x+2 | D. | y=2x+3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com