
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )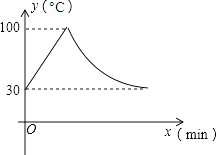
A.7:20
B.7:30
C.7:45
D.7:50
【答案】A
【解析】解:∵开机加热时每分钟上升10℃,
∴从30℃到100℃需要7分钟,
设一次函数关系式为:y=k1x+b,
将(0,30),(7,100)代入y=k1x+b得k1=10,b=30
∴y=10x+30(0≤x≤7),令y=50,解得x=2;
设反比例函数关系式为:y= ![]() ,
,
将(7,100)代入y= ![]() 得k=700,∴y=
得k=700,∴y= ![]() ,
,
将y=30代入y= ![]() ,解得x=
,解得x= ![]() ;
;
∴y= ![]() (7≤x≤
(7≤x≤ ![]() ),令y=50,解得x=14.
),令y=50,解得x=14.
所以,饮水机的一个循环周期为 ![]() 分钟.每一个循环周期内,在0≤x≤2及14≤x≤
分钟.每一个循环周期内,在0≤x≤2及14≤x≤ ![]() 时间段内,水温不超过50℃.
时间段内,水温不超过50℃.
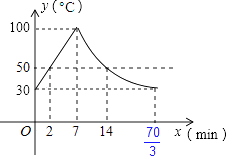
逐一分析如下:
选项A:7:20至8:45之间有85分钟.85﹣ ![]() ×3=15,位于14≤x≤
×3=15,位于14≤x≤ ![]() 时间段内,故可行;
时间段内,故可行;
选项B:7:30至8:45之间有75分钟.75﹣ ![]() ×3=5,不在0≤x≤2及14≤x≤
×3=5,不在0≤x≤2及14≤x≤ ![]() 时间段内,故不可行;
时间段内,故不可行;
选项C:7:45至8:45之间有60分钟.60﹣ ![]() ×2=
×2= ![]() ≈13.3,不在0≤x≤2及14≤x≤
≈13.3,不在0≤x≤2及14≤x≤ ![]() 时间段内,故不可行;
时间段内,故不可行;
选项D:7:50至8:45之间有55分钟.55﹣ ![]() ×2=
×2= ![]() ≈8.3,不在0≤x≤2及14≤x≤
≈8.3,不在0≤x≤2及14≤x≤ ![]() 时间段内,故不可行.
时间段内,故不可行.
综上所述,四个选项中,唯有7:20符合题意.
故答案为:A.
根据实际情况由开机加热时每分钟上升10℃,得到从30℃到100℃需要7分钟,设出一次函数关系式为y=k1x+b,将(0,30),(7,100)代入y=k1x+bk1=10,求出b=30,解得x=2;设反比例函数关系式为y= ![]() ,将(7,100)代
,将(7,100)代![]() 入得k=700,得到解析式
入得k=700,得到解析式![]() ,求出饮水机的一个循环周期为的时间,每一个循环周期内,分时间段分析,得出结论.
,求出饮水机的一个循环周期为的时间,每一个循环周期内,分时间段分析,得出结论.


科目:初中数学 来源: 题型:
【题目】如图,下列关系错误的是( )

A. ∠AOC=∠AOB+∠BOC
B. ∠AOC=∠AOD-∠COD
C. ∠AOC=∠AOB+∠BOD-∠BOC
D. ∠AOC=∠AOD-∠BOD+∠BOC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.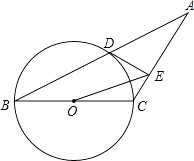
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步推进青少年毒品预防教育“627“工程,切实提高广大青少年识毒、防毒、拒毒的意识和能力,我市高度重视全国青少年禁毒知识竞赛活动.针对某校七年级学生的知识竞赛成绩绘制了如图不完整的统计图表.

知识竞赛成绩频数分布表
组别 | 成绩(分数) | 人数 |
A | 95≤x<100 | 300 |
B | 90≤x<95 | a |
C | 85≤x<90 | 150 |
D | 80≤x<85 | 200 |
E | 75≤x<80 | b |
根据所给信息,解答下列问题.
(1)a=____,b=____.
(2)请求出C组所在扇形统计图中的圆心角的度数.
(3)补全知识竞赛成绩频数分布直方图.
(4)已知我市七年级有180000名学生,请估算全市七年级知识竞赛成绩低于80分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天小明和同学们去郊外爬山,得到如下数据:
爬坡长度x(m) | 40 | 80 | 120 | 160 | 200 | 240 |
爬坡时间t(min) | 2 | 5 | 9 | 14 | 20 | 30 |
(1)当爬到120 m时,所用时间是多少?
(2)爬坡速度随时间是怎样变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,淇淇的爸爸去参加一个聚会,淇淇坐在汽车上用所学知识绘制了一张反映汽车速度与时间的关系图,第二天,淇淇拿着这张图给同学看,并向同学提出如下问题,你能回答吗?
(1)在上述变化过程中,自变量是什么?因变量是什么?
(2)汽车从出发到最后停止共经过了多长时间?它的最高时速是多少?
(3)汽车在哪段时间保持匀速行驶?速度是多少?
(4)用语言大致描述这辆汽车的行驶情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
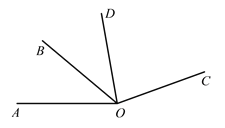
【题目】几何计算:
如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:因为∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=![]() __________=__________°
__________=__________°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com