2
分析:由DE是△ABC的中位线,△ABC的面积为48cm
2,易求得△ADE的面积,然后过点E作EF∥AB交CN于F,易求得△ACN的面积,即可求得△BCN的面积与MN:CN的值,又由△DMN∽△BCN,根据相似三角形的面积比等于相似比的平方,即可求得△DMN的面积.
解答:∵DE是△ABC的中位线,
∴DE∥BC,DE=

BC,
∴△ADE∽△ABC,
∴
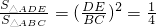
,
∵S
△ABC=48cm
2,
∴S
△ADE=12cm
2,
∴S
四边形BCED=S
△ABC-S
△ADE=48-12=36(cm
2),
过点E作EF∥AB交CN于F,
∴EF是△ACN的中位线,∠NDM=∠FEM,
∴CF=FN,

EF=

AN,
∵M是DE的中点,
∴DM=EM,
在△NDM和△FEM中,

,
∴△NDM≌△FEM(ASA),
∴FM=MN,S
四边形AEFN=S
△ADE=12cm
2,
∴MN:CN=1:4,
∵EF∥AB,
∴△CEF∽△CAN,
∴

,
∴S
△ACN:S
四边形AEFN=4:3,
∴S
△ACN=16cm
2,
∴S
△BCN=S
△ABC-S
△ACN=32cm
2,
∵DE∥BC,
∴△DMN∽△BCN,
∴

,
∴S
△DMN=2cm
2.
故答案为:2.
点评:此题考查了相似三角形的判定与性质以及三角形中位线的性质.此题难度较大,注意准确作出辅助线是解此题的关键,注意相似三角形面积的比等于相似比的平方定理的应用.

 如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为________cm2.
如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为________cm2. BC,
BC,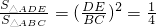 ,
, EF=
EF= AN,
AN, ,
, ,
, ,
,

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案