
【题目】某宾馆有 50 个房间供游客居住,当每个房间的定价为每天 160 元时,房间会全部住满,当每个房间每天的定价每增加 10 元时,就会有一个房间空闲,如果游客居住房间, 宾馆需对每个房间每天支出 20 元的各种费用.设每个房间的定价为 x 元时,相应的住房数为 y 间.
(1)求 y 与 x 的函数关系式;
(2)定价为多少时宾馆当天利润 w 最大?并求出一天的最大利润;
(3)若老板决定每住进去一间房就捐出 a 元(a≤30)给当地福利院,同时要保证房间定价 x 在 160 元至 350 元之间波动时(包括两端点),利润 w 随 x 的增大而增大,求 a 的取值范围
科目:初中数学 来源: 题型:
【题目】在生活中,有很多函数并不一定存在解析式,对于这样的函数,我们可以通过列表和图象来对它可能存在的性质进行探索,例如下面这样一个问题:
已知y是x的函数,下表是y与x的几组对应值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
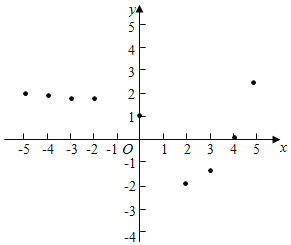
下面是小孙同学的探究过程,请补充完整;
(1)如图,在平面之间坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出函数的图象:
(2)根据画出的函数图象回答:
①x=﹣1时,对应的函数值y的为 ;
②若函数值y>0,则x的取值范围是 ;
③写出该函数的一条性质(不能与前面已有的重复): .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小刚家,菜地,稻田在同一条直线上.小刚从家去菜地浇水,又去稻田除草,然后回家.如图反映了这个过程中,小刚离家的距离y与时间x之间的对应关系.如果菜地和稻田的距离为akm,小刚在稻田除草比在菜地浇水多用了bmin,则a,b的值分别为( )
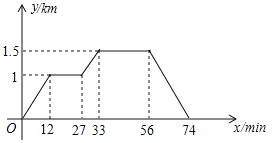
A.1,8B.0.5,12C.1,12D.0.5,8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:其中,正确的个数有( )
①b2﹣4ac<0;②a﹣b+c<0;③abc>0;④m>﹣2.
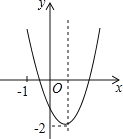
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子中放入四张卡片,每张卡片上都写有一个数字,分别是2,1,0,1.卡片除数字不同外其它均相同,从中随机抽取两张卡片,抽取的两张卡片上数字之积为 0的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个阳光明媚的上午,小明和小兰相约从鲁能巴蜀中学沿相同的路线去龙头寺公园写生,小明出发5分钟后小兰才出发,此时小明发现忘记带颜料,立即按原速原路回学校拿颜料,小明拿到颜料后,以比原速提髙20%的速度赶去公园,结果还是比小兰晚2分钟到公园(小明拿颜料的时间忽略不计).在整个过程中,小兰保持匀速运动,小明提速前后也分别保持匀速运动,如图所示是小明与小兰之间的距离![]() (米)与小明出发的时间
(米)与小明出发的时间![]() (分钟)之间的函数图象,则学校到公园的距离为_______米.
(分钟)之间的函数图象,则学校到公园的距离为_______米.
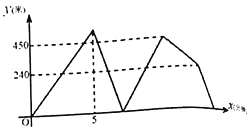
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,在平面直角坐标系中,二次函数![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
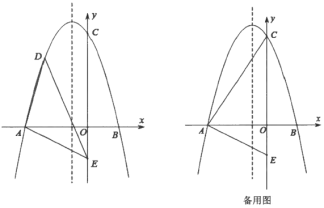
(1)求二次函数的表达式;
(2)点![]() 是第二象限内的点抛物线上一动点
是第二象限内的点抛物线上一动点
①求![]() 面积最大值并写出此时点
面积最大值并写出此时点![]() 的坐标;
的坐标;
②若![]() ,求此时点
,求此时点![]() 坐标;
坐标;
(3)连接![]() ,点
,点![]() 是线段
是线段![]() 上的动点.连接
上的动点.连接![]() ,把线段
,把线段![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,点
,点![]() 是点
是点![]() 的对应点.当动点
的对应点.当动点![]() 从点
从点![]() 运动到点
运动到点![]() ,则动点
,则动点![]() 所经过的路径长等于______(直接写出答案)
所经过的路径长等于______(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
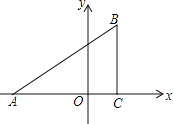
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.
(1)写出点B的坐标;
(2)在x轴上找一点D,连接BD,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如果点P从点A出发,以2cm/秒的速度沿AB向点B运动,同时点Q从点D出发,以1cm/秒的速度沿DA向点A运动.当一个点停止运动时,另一个点也随之停止运动.设运动时间为t.问是否存在这样的t使得△APQ与△ADB相似?如存在,请求出t的值;如不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com