
【题目】如图,已知![]() ,
,![]() ,
,![]() .试说明直线
.试说明直线![]() 与
与![]() 垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).
垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).

理由:![]() ,(已知)
,(已知)
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
又![]() ,(已知)
,(已知)
![]()
![]() .(等量代换)
.(等量代换)
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() ,(已知)
,(已知)
![]() ,
,![]() ,
,
![]()
![]() .
.
【答案】GD,AC,同位角相等,两直线平行;∠DAC,两直线平行,内错角相等;∠DAC;AD,EF,同旁内角互补,两直线平行;两直线平行,同位角相等;AD,BC.
【解析】
结合图形,根据平行线的判定和性质逐一进行填空即可.
∵∠1=∠C,(已知)
∴GD∥AC,(同位角相等,两直线平行)
∴∠2=∠DAC.(两直线平行,内错角相等)
又∵∠2+∠3=180°,(已知)
∴∠3+∠DAC=180°.(等量代换)
∴AD∥EF,(同旁内角互补,两直线平行)
∴∠ADC=∠EFC.(两直线平行,同位角相等)
∵EF⊥BC,(已知 )
∴∠EFC=90°,
∴∠ADC=90°,
∴AD⊥BC.
故答案为:GD,AC,同位角相等,两直线平行;∠DAC,两直线平行,内错角相等;∠DAC;AD,EF,同旁内角互补,两直线平行;两直线平行,同位角相等;AD,BC.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD的边长为5,点E在边AB上,AE=3,延长DA至点F,使AF=AE,连结EF.将△AEF绕点A顺时针旋转![]() (0°<
(0°<![]() <90°),如图2所示,连结DE、BF.
<90°),如图2所示,连结DE、BF.
(1)请直接写出DE的取值范围:_______________________;
(2)试探究DE与BF的数量关系和位置关系,并说明理由;
(3)当DE=4时,求四边形EBCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,O为坐标原点,抛物线y=﹣ ![]() ax2+
ax2+ ![]() ax+3a(a≠0)与x轴交于A和点B(A在左,B在右),与y轴的正半轴交于点C,且OB=OC.
ax+3a(a≠0)与x轴交于A和点B(A在左,B在右),与y轴的正半轴交于点C,且OB=OC.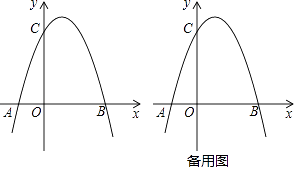
(1)求抛物线的解析式;
(2)若D为OB中点,E为CO中点,动点F在y轴的负半轴上,G在线段FD的延长线上,连接GE、ED,若D恰为FG中点,且S△GDE= ![]() ,求点F的坐标;
,求点F的坐标;
(3)在(2)的条件下,动点P在线段OB上,动点Q在OC的延长线上,且BP=CQ.连接PQ与BC交于点M,连接GM并延长,GM的延长线交抛物线于点N,连接QN、GP和GB,若角满足∠QPG﹣∠NQP=∠NQO﹣∠PGB时,求NP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )
A.它的图象与x轴有两个交点
B.方程x2﹣2mx=3的两根之积为﹣3
C.它的图象的对称轴在y轴的右侧
D.x<m时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
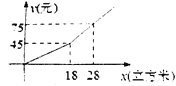
【题目】为了增强人们的节约用水意识,环节城市用水压力。某市规定,每月用水18立方米以内(含18立方米)和用水18立方米以上采取两种不同的收费标准.下图为该市的用户每月应交水费y(元)关于用水量x(立方米)的函数图像.思考并回答下列问题:
(1)求出用水量小于18立方米时,每月应交水费y(元)关于用水量x(立方米)的函数表达式.
(2)若小明家某月交水费81元,则这个月用水量为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.

(1)图②中的阴影部分的面积为________;
(2)观察图②,三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系是________;
(3)观察图③,你能得到怎样的代数等式呢?
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n);
(5)若x+y=﹣6,xy=2.75,求x﹣y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com