
【题目】如图1,已知正方形ABCD的边长为5,点E在边AB上,AE=3,延长DA至点F,使AF=AE,连结EF.将△AEF绕点A顺时针旋转![]() (0°<
(0°<![]() <90°),如图2所示,连结DE、BF.
<90°),如图2所示,连结DE、BF.
(1)请直接写出DE的取值范围:_______________________;
(2)试探究DE与BF的数量关系和位置关系,并说明理由;
(3)当DE=4时,求四边形EBCD的面积.

【答案】(1)DE的取值范围:2<DE<![]() ;(2)DE=BF,DE⊥BF,理由详见解析;(3)当DE=4时,四边形EBCD的面积为14.5.
;(2)DE=BF,DE⊥BF,理由详见解析;(3)当DE=4时,四边形EBCD的面积为14.5.
【解析】
(1)根据点E在AB边上和在AD边上时DE分别为最大值和最小值解答即可;(2)延长DE,交AB于点G,交BF于点H,易得∠EAD=∠FAB,根据SAS可证明△EAD≌△FAB,即可得DE=BF,∠ADE=∠ABF,根据∠AGD=∠BGH,∠ADE+∠AGD=90°可得∠ABF+∠BGH=90°进而可得∠BHG=90° 即DE⊥BF;(3)由AE=3,DE=4,AD=5可得△AED是直角三角形,由(2)得△EAD≌△FAB,可知∠AFB=∠AED=90°,BF=DE=4,![]() ,由∠EAF=90°可得AE//BF,进而可求出四边形ABEF得面积,根据
,由∠EAF=90°可得AE//BF,进而可求出四边形ABEF得面积,根据![]()
![]() 即可得答案.
即可得答案.
(1)∵点E在AB边上和在AD边上时DE分别为最大值和最小值,
∴![]() ,5-3=2,
,5-3=2,
∴DE的取值范围:2<DE<![]() ;
;
(2)DE=BF,DE⊥BF,理由如下:
延长DE,交AB于点G,交BF于点H
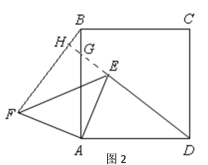
∵∠BAD=∠FAE=90°
即∠BAE+∠EAD=∠BAE+∠FAB=90°
∴∠EAD=∠FAB
在△EAD和△FAB中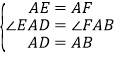
∴△EAD≌△FAB
∴DE=BF,∠ADE=∠ABF
又∵∠AGD=∠BGH,∠ADE+∠AGD=90°
∴∠ABF+∠BGH=90°
∴∠BHG=90° 即DE⊥BF
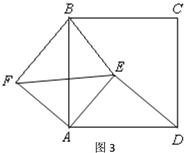
(3)∵AE=3,DE=4,AD=5
∴![]()
∴△ADE为直角三角形,∠AED=90°
由(2)得△EAD≌△FAB
∴∠AFB=∠AED=90°,BF=DE=4,![]()
又∵∠EAF=90°
∴AE∥BF
∴四边形AEBF的面积为:![]() =
=![]() =10.5
=10.5
∴![]() =10.5
=10.5
∴![]()
![]() 52-10.5=14.5
52-10.5=14.5
答:当DE=4时,四边形EBCD的面积为14.5.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( )

A.120°B.135°C.150°D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有足够多的正方形和长方形的卡片,如图1所示,请运用拼图的方法,选取相应种类和数量的卡片,按要求回答下列问题.
(1)根据图2,利用面积的不同表示方法,写出一个代数恒等式:______________________;
(2)若要拼成一个长为![]() ,宽为
,宽为![]() 的长方形,则需要甲卡片____张,乙卡片____张,丙卡片____张;
的长方形,则需要甲卡片____张,乙卡片____张,丙卡片____张;

(3)请用画图结合文字说明的方式来解释:![]() ≠
≠![]() (
(![]() ≠0,
≠0,![]() ≠0).
≠0).
查看答案和解析>>
科目:初中数学 来源: 题型:
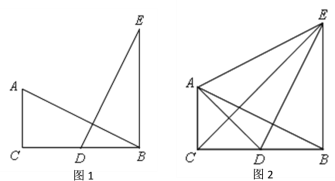
【题目】如图1,在△ABC中,∠ACB=90°,AC=![]() BC,点D为BC的中点,AB =DE,BE∥AC.
BC,点D为BC的中点,AB =DE,BE∥AC.
(1)求证:△ABC≌△DEB;
(2)连结AD、AE、CE,如图2.
①求证:CE是∠ACB的角平分线;
②请判断△ABE是什么特殊形状的三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论错误的是( )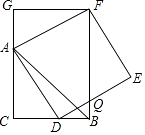
A.AC=FG
B.S△FAB:S四边形CBFG=1:2
C.AD2=FQAC
D.∠ADC=∠ABF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() .试说明直线
.试说明直线![]() 与
与![]() 垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).
垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).

理由:![]() ,(已知)
,(已知)
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
又![]() ,(已知)
,(已知)
![]()
![]() .(等量代换)
.(等量代换)
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() ,(已知)
,(已知)
![]() ,
,![]() ,
,
![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com