
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为 . 
【答案】![]()
【解析】解:在△CAD中,∵M、N分别是AC、CD的中点, 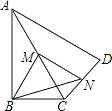
∴MN∥AD,MN= ![]() AD,
AD,
在Rt△ABC中,∵M是AC中点,
∴BM= ![]() AC,
AC,
∵AC=AD,
∴MN=BM,
∵∠BAD=60°,AC平分∠BAD,
∴∠BAC=∠DAC=30°,
∴BM= ![]() AC=AM=MC,
AC=AM=MC,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,
∵MN∥AD,
∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,
∴MN=BM= ![]() AC=1,
AC=1,
∴BN= ![]() .
.
所以答案是: ![]() .
.
【考点精析】关于本题考查的直角三角形斜边上的中线和勾股定理的概念,需要了解直角三角形斜边上的中线等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】如图(1), ![]() ,.点P在线段AB上以
,.点P在线段AB上以![]() 的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为
的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为![]() .
.
(1)若点Q的运动速度与点P的运动速度相等,当![]() 时,
时, ![]() 与
与![]() 是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“![]() ,”为改“”,其他条件不变.设点Q的运动速度为
,”为改“”,其他条件不变.设点Q的运动速度为![]() ,是否存在实数x,使得
,是否存在实数x,使得![]() 与
与![]() 全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
全等?若存在,求出相应的x、t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD的边长为5,点E在边AB上,AE=3,延长DA至点F,使AF=AE,连结EF.将△AEF绕点A顺时针旋转![]() (0°<
(0°<![]() <90°),如图2所示,连结DE、BF.
<90°),如图2所示,连结DE、BF.
(1)请直接写出DE的取值范围:_______________________;
(2)试探究DE与BF的数量关系和位置关系,并说明理由;
(3)当DE=4时,求四边形EBCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火车站有某公司待运的甲种货物1530吨,乙种货物1150吨,现计划用50节A,B两种型号的车厢将这批货物运至北京,已知每节A型车厢的运费是0.5万元,每节B型车厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型车厢,甲种货物25吨和乙种货物35吨可装满一节B型车厢,按此要求安排A,B两种车厢的节数,共有哪几种方案?请你设计出所有方案,并说明哪种方案的运费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场为推销某一品牌运动服,先做了市场调查,得到数据如下表:
卖出价格x(元/件) | 50 | 51 | 52 | 53 |
销售量P(件) | 500 | 490 | 480 | 470 |
则P与x的函数关系式为________,当卖出价格为60元时,销售量为_______件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,O为坐标原点,抛物线y=﹣ ![]() ax2+
ax2+ ![]() ax+3a(a≠0)与x轴交于A和点B(A在左,B在右),与y轴的正半轴交于点C,且OB=OC.
ax+3a(a≠0)与x轴交于A和点B(A在左,B在右),与y轴的正半轴交于点C,且OB=OC.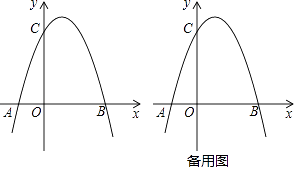
(1)求抛物线的解析式;
(2)若D为OB中点,E为CO中点,动点F在y轴的负半轴上,G在线段FD的延长线上,连接GE、ED,若D恰为FG中点,且S△GDE= ![]() ,求点F的坐标;
,求点F的坐标;
(3)在(2)的条件下,动点P在线段OB上,动点Q在OC的延长线上,且BP=CQ.连接PQ与BC交于点M,连接GM并延长,GM的延长线交抛物线于点N,连接QN、GP和GB,若角满足∠QPG﹣∠NQP=∠NQO﹣∠PGB时,求NP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com