
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������y=�� ![]() ax2+
ax2+ ![]() ax+3a��a��0����x�ύ��A�͵�B��A����B���ң�����y��������ύ�ڵ�C����OB=OC��
ax+3a��a��0����x�ύ��A�͵�B��A����B���ң�����y��������ύ�ڵ�C����OB=OC��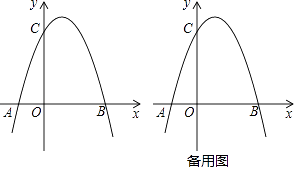
��1���������ߵĽ���ʽ��
��2����DΪOB�е㣬EΪCO�е㣬����F��y��ĸ������ϣ�G���߶�FD���ӳ����ϣ�����GE��ED����DǡΪFG�е㣬��S��GDE= ![]() �����F�����ꣻ
�����F�����ꣻ
��3���ڣ�2���������£�����P���߶�OB�ϣ�����Q��OC���ӳ����ϣ���BP=CQ������PQ��BC���ڵ�M������GM���ӳ���GM���ӳ��߽��������ڵ�N������QN��GP��GB�����������QPG����NQP=��NQO����PGBʱ����NP�ij���
���𰸡�
��1���⣺��y=0����ã�y=�� ![]() ax2+
ax2+ ![]() ax+3a��
ax+3a��
��a��0��
�ੁ ![]() x2+
x2+ ![]() x+3=0��
x+3=0��
��ã�x1=�� ![]() ��x2=6��
��x2=6��
��A���� ![]() ��0����B��6��0����
��0����B��6��0����
��OB=6��
�߽�x=0���������ߵĽ���ʽ�ã�y=3a��
��C��0��3a����
��OC=3a��
��OB=0C��
��3a=6��
��ã�a=2��
�������ߵĽ���ʽΪy=�� ![]() x2+
x2+ ![]() x+6��
x+6��
��2���⣺��ͼ1��ʾ������GB��
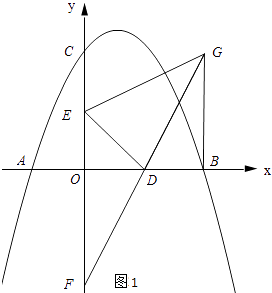
��E��D�ֱ���OC��0B���е㣬
��OE=3��OD=BD��
�ڡ�ODF�͡�GDB�У�
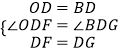 ��
��
���ODF�ա�GDB��
��BG=OF����GBD=��FOD=90�㣬
��S��EDG=S��EFG��S��EFD��
�� ![]() EFOB��
EFOB�� ![]() EFOD=
EFOD= ![]() ����3EF��
����3EF�� ![]() EF=
EF= ![]() ����ã�EF=9��
����ã�EF=9��
��OF=EF��OE=9��3=6��
��F��0����6����
��3���⣺��ͼ2��ʾ������P��PT��y�ᣬ��BC���T������N��NR��y�ᣬ����ΪR��NH��x����H��
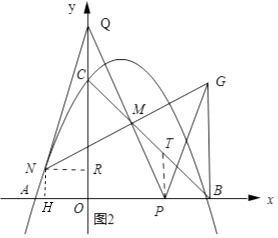
��TP��OQ��
���MPT=��MQC����PTM=��QCM��
��OB=0C=6��
���OCB=��OBC=45�㣬
���PBT=��PTB=45�㣬
��PT=PB=CQ��
�ڡ�PTM�͡�QCM�У�
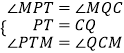 ��
��
���PTM�ա�QCM��
��PM=QM��
��GB��x�ᣬ
��BG��y���PT��
���BGP=��TPG��
�ߡ�QPG����NQO=��NQP����PGB��
���QPT+��TPG����NQO=��NQO+��OQP����PCB��
�ߡ�QPT=��OQP����TPG=��PGB��
��2��TPG=2��NQO��
���TPG=��NQO��
���NQP=��GPQ��
�ڡ�NMQ�͡�GMP�У� 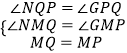 ��
��
���NMQ�ա�GMP��
��NQ=GP��
��Rt��QNR��Rt��GPB�� 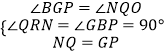 ��
��
���QNR�ա�GPB��
��QM=BG=6��NR=PB=CQ��
��N��t���� ![]() t2+
t2+ ![]() t+6����
t+6����
��QO=QC+CO=QR+RO��
��QC=RO��
��NR=RO��
�ੁt=�� ![]() t2+
t2+ ![]() t+6����ã�t1=��2��t2=8����ȥ����
t+6����ã�t1=��2��t2=8����ȥ����
��N����2��2����
��NH=2��OH=NR=2��
��PH=OB=6��
��PN= ![]() =2
=2 ![]() ��
��
���߶�NP�ij�Ϊ2 ![]() ��
��
�������� ��1����y=0����õ�A,B�����꣬��x=0���������ߵĽ���ʽ��õ�C�����꣬Ȼ�����OB=OC�����a��ֵ���Ӷ��õ������ߵĽ���ʽ��
��2������GB����������SAS֤����ODF�ա�GDB���Ӷ��õ�BG=OF������������S��EDG=S��EFG��S��EFD�����EF�ij����Ӷ��õ�BG�ij����ʴ˿ɵõ���F�����ꣻ
(3)����P��PT��y�ᣬ��BC���T������N��NR��y�ᣬ����ΪR��NH��x����H������֤��PT=PB=CQ��Ȼ������SAS֤����PTM�ա�QCM�����ǵõ�PM=QM����֤����NMQ�ա�GMP���õ�NQ=GP����֤����QNR�ա�GPB���õ�NR=RO���Ӷ��г�����t�ķ��̣����NR�ij��������Rt��NHP�����ݹ��ɶ����ó����ۡ�
�����㾫����ͨ��������ù��ɶ����ĸ������ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������㹻��������κͳ����εĿ�Ƭ����ͼ1��ʾ��������ƴͼ�ķ�����ѡȡ��Ӧ����������Ŀ�Ƭ����Ҫ��ش��������⣮
��1������ͼ2����������IJ�ͬ��ʾ������д��һ���������ʽ��______________________��
��2����Ҫƴ��һ����Ϊ![]() ����Ϊ
����Ϊ![]() �ij����Σ�����Ҫ��Ƭ____�ţ��ҿ�Ƭ____�ţ�����Ƭ____�ţ�
�ij����Σ�����Ҫ��Ƭ____�ţ��ҿ�Ƭ____�ţ�����Ƭ____�ţ�

��3�����û�ͼ�������˵���ķ�ʽ�����ͣ�![]() ��
��![]() ��
��![]() ��0��
��0��![]() ��0����
��0����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���ABC=90�㣬AC=AD��M��N�ֱ�ΪAC��CD���е㣬����BM��MN��BN����BAD=60�㣬ACƽ�֡�BAD��AC=2��BN�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
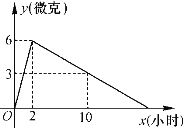
����Ŀ��ijҽԺ�з���һ����ҩ������ҩЧʱ���֣�������˰��涨�������ã���ô��ҩ2Сʱ��ѪҺ�к�ҩ����ߣ���ÿ����6�ˣ�������˥����10Сʱ��ѪҺ�к�ҩ��Ϊÿ����3�ˣ�ÿ����ѪҺ�к�ҩ��y(��)��ʱ��x(Сʱ)�ı仯��ͼ��ʾ�������˰��涨������ҩ��
(1)��ҩ��СʱѪҺ�к�ҩ����ߣ��ﵽÿ����ѪҺ�к�ҩ�����ˣ�
(2)�ڷ�ҩ����Сʱ��ѪҺ�еĺ�ҩ�������ߣ��ڼ�Сʱ��ѪҺ�еĺ�ҩ����˥����
(3)��ҩ��10Сʱʱ��ѪҺ�к�ҩ���Ƕ����ˣ�
(4)��ҩ��Сʱ������Ч��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʽ�ֽ⣺
��1�� ![]()
��2��3ax2+6axy+3ay2
��3��16��x��1��2 ��9��x��2��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǰ���ѧϰ��ѧ����Ҫ���ߣ���һ�����ǰ��е�����ֱ�����ǰ��ֱ�Ƕ���![]() ����ͼ��ʽ������һ�𣬵�
����ͼ��ʽ������һ�𣬵�![]() �ҵ�
�ҵ�![]() ��ֱ��
��ֱ��![]() ���Ϸ�ʱ������������⣺��������ʾ��
���Ϸ�ʱ������������⣺��������ʾ��![]() ��
��![]() ��
��![]() ��
��

��1������![]() ����
����![]() �Ķ���Ϊ������
�Ķ���Ϊ������
����![]() ����
����![]() �Ķ���Ϊ������
�Ķ���Ϊ������
��2���ɣ�1������![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
��3�����������ǰ��Ƿ����һ�����ƽ�У������ڣ���ֱ��д��![]() �ĽǶ����п��ܵ�ֵ������˵�����ɣ����������ڣ���˵�����ɣ�
�ĽǶ����п��ܵ�ֵ������˵�����ɣ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��
��![]() ����˵��ֱ��
����˵��ֱ��![]() ��
��![]() ��ֱ������������Ľ����̵Ŀո�����ջ�����������д���ɣ���
��ֱ������������Ľ����̵Ŀո�����ջ�����������д���ɣ���

���ɣ�![]() ������֪��
������֪��
![]() ����
����![]() ������
������![]() ����
����![]()
![]() ������
������![]() ����
����![]()
��![]() ������֪��
������֪��
![]() ����
����![]() ��������������
��������������
![]() ����
����![]() ������
������![]() ����
����![]()
![]() ��
��![]() ����
����![]()
![]() ������֪��
������֪��
![]() ��
��![]() ��
��
![]() ����
����![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
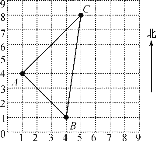
����Ŀ����ͼ��ʾ��ijѧУ��ƽ��ͼ��һ���֣�����A��������¥��B����ʵ��¥��C����ͼ��ݣ�������������ÿ��С�����εı߳�Ϊ1���Խ��ͼ�λش��������⣺
(1)��(1��4)��ʾ����¥A��λ�ã���ôʵ��¥B��ͼ���C��λ����α�ʾ��
(2)����¥��֮��������·AC��AB��BC������֪������·�ij��ȴ������й�ϵ��AC2��AB2��BC2.����B��A�ľ���Ϊ3![]() �����Ƕ�ƫ������Ϊ����������ƫ�Ϸ���Ϊ����������B�������A���λ�ü���(��45����3
�����Ƕ�ƫ������Ϊ����������ƫ�Ϸ���Ϊ����������B�������A���λ�ü���(��45����3![]() )����ô��C�������A���λ�ÿ���α�ʾ��
)����ô��C�������A���λ�ÿ���α�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������κ���ͼ��Ķ�����ͬ�����ڴ�С��ͬ�������ڷ����෴��������������κ���Ϊ���Գƶ��κ�������
��1����д�����κ���y=2��x��2��2+1�ġ��Գƶ��κ�������
��2����֪����x�Ķ��κ���y1=x2��3x+1��y2=ax2+bx+c����y1��y2��y1��Ϊ���Գƶ��κ�����������y2�ı���ʽ�����������3��x��3ʱ��y2�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com