
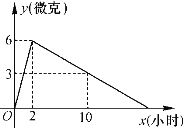
【题目】某医院研发了一种新药,试验药效时发现,如果成人按规定剂量服用,那么服药2小时后,血液中含药量最高,达每毫升6微克,接着逐渐衰减,10小时后血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后:
(1)服药后几小时血液中含药量最高?达到每毫升血液中含药多少微克?
(2)在服药几个小时后,血液中的含药量逐渐升高?在几小时后,血液中的含药量逐渐衰减?
(3)服药后10小时时,血液中含药量是多少微克?
(4)服药几小时后即已无效?
科目:初中数学 来源: 题型:
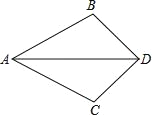
【题目】如图,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“SAS”需添加条件________;
(2)根据“ASA”需添加条件________;
(3)根据“AAS”需添加条件________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火车站有某公司待运的甲种货物1530吨,乙种货物1150吨,现计划用50节A,B两种型号的车厢将这批货物运至北京,已知每节A型车厢的运费是0.5万元,每节B型车厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型车厢,甲种货物25吨和乙种货物35吨可装满一节B型车厢,按此要求安排A,B两种车厢的节数,共有哪几种方案?请你设计出所有方案,并说明哪种方案的运费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场为推销某一品牌运动服,先做了市场调查,得到数据如下表:
卖出价格x(元/件) | 50 | 51 | 52 | 53 |
销售量P(件) | 500 | 490 | 480 | 470 |
则P与x的函数关系式为________,当卖出价格为60元时,销售量为_______件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 ![]()
![]() 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 ![]() 天的总成本为
天的总成本为 ![]() 万元;放养
万元;放养 ![]() 天的总成本为
天的总成本为 ![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是 ![]() 万元,收购成本为
万元,收购成本为 ![]() 万元,求
万元,求 ![]() 和
和 ![]() 的值;
的值;
(2)设这批淡水鱼放养 ![]() 天后的质量为
天后的质量为 ![]() (
( ![]() ),销售单价为
),销售单价为 ![]() 元/
元/ ![]() .根据以往经验可知:
.根据以往经验可知: ![]() 与
与 ![]() 的函数关系为
的函数关系为 ![]() ;
; ![]() 与
与 ![]() 的函数关系如图所示.
的函数关系如图所示.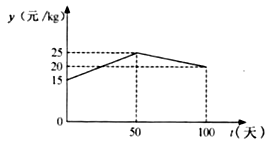
①分别求出当 ![]() 和
和 ![]() 时,
时, ![]() 与
与 ![]() 的函数关系式;
的函数关系式;
②设将这批淡水鱼放养 ![]() 天后一次性出售所得利润为
天后一次性出售所得利润为 ![]() 元,求当
元,求当 ![]() 为何值时,
为何值时, ![]() 最大?并求出最大值.(利润=销售总额-总成本)
最大?并求出最大值.(利润=销售总额-总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,O为坐标原点,抛物线y=﹣ ![]() ax2+
ax2+ ![]() ax+3a(a≠0)与x轴交于A和点B(A在左,B在右),与y轴的正半轴交于点C,且OB=OC.
ax+3a(a≠0)与x轴交于A和点B(A在左,B在右),与y轴的正半轴交于点C,且OB=OC.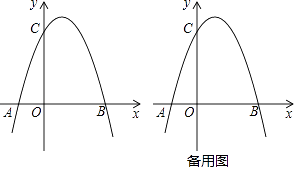
(1)求抛物线的解析式;
(2)若D为OB中点,E为CO中点,动点F在y轴的负半轴上,G在线段FD的延长线上,连接GE、ED,若D恰为FG中点,且S△GDE= ![]() ,求点F的坐标;
,求点F的坐标;
(3)在(2)的条件下,动点P在线段OB上,动点Q在OC的延长线上,且BP=CQ.连接PQ与BC交于点M,连接GM并延长,GM的延长线交抛物线于点N,连接QN、GP和GB,若角满足∠QPG﹣∠NQP=∠NQO﹣∠PGB时,求NP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )
A.它的图象与x轴有两个交点
B.方程x2﹣2mx=3的两根之积为﹣3
C.它的图象的对称轴在y轴的右侧
D.x<m时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是( )
A.2
B.![]()
C.3
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com