
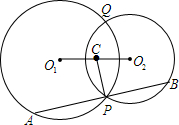
 己知:如图.⊙01与⊙O2相交于点P、Q.点C是线段O1O2的中点,AB过点P且与CP垂直,点A、B分别是AB与⊙O1、⊙O2的交点,求证:AP=BP.
己知:如图.⊙01与⊙O2相交于点P、Q.点C是线段O1O2的中点,AB过点P且与CP垂直,点A、B分别是AB与⊙O1、⊙O2的交点,求证:AP=BP.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
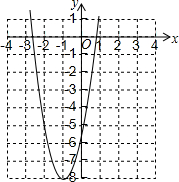 这是小明在阅读一本关于函数的课外读物时看到的一段文字:“由图象知,当x=-1时,二次函数y=ax2+6x-5的值最小”,你能写出a的值吗?
这是小明在阅读一本关于函数的课外读物时看到的一段文字:“由图象知,当x=-1时,二次函数y=ax2+6x-5的值最小”,你能写出a的值吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
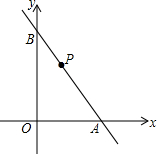 如图所示,已知直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A,B两点,点P是线段AB上的一个动点,连结OP,把△ABO分成两个小三角形,分别是△AOP和△BOP,当AP的长为多少时,△AOP和△BOP中至少有一个是等腰三角形?
如图所示,已知直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A,B两点,点P是线段AB上的一个动点,连结OP,把△ABO分成两个小三角形,分别是△AOP和△BOP,当AP的长为多少时,△AOP和△BOP中至少有一个是等腰三角形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
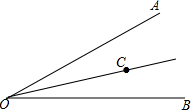 如图,OC平分∠AOB.
如图,OC平分∠AOB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
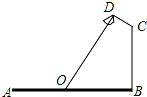 如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.
如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com