
ЎҫМвДҝЎҝОТКРОӘҙҙҪЁЎ°№ъјТј¶ЙӯБЦіЗКРЎұЈ¬Хюё®ҫц¶Ё¶ФҪӯұЯТ»ҙҰ·ПЖъ»ДөШҪшРРВМ»ҜЈ¬ТӘЗуФФЦІјЧЎўТТБҪЦЦІ»Н¬өДКчГз№І6000ҝГЈ¬ЗТјЧЦЦКчГзІ»өГ¶аУЪТТЦЦКчГзЈ®ДііР°ьЙМТФ26НтФӘөДұЁјЫЦРұкіР°ьБЛХвПо№ӨіМЈ®ёщҫЭөчІйј°Па№ШЧКБПұнГчЈәТЖФФТ»ҝГКчГзөДЖҪҫщ·СУГОӘ8ФӘЈ¬јЧЎўТТБҪЦЦКчГзөД№әВтјЫј°іЙ»оВКИзұнЈә

Йи№әВтјЧЦЦКчГзxҝГЈ¬іР°ьЙМ»сөГөДАыИуОӘyФӘЈ®ЗлёщҫЭТФЙПРЕПўҪвҙрПВБРОКМвЈә
(1) ЙиyУлxЦ®јдөДәҜКэ№ШПөКҪЈ¬ІўРҙіцЧФұдБҝxөДИЎЦө·¶О§Ј»
(2) іР°ьЙМТӘ»сөГІ»өНУЪЦРұкјЫ16%өДАыИуЈ¬УҰИзәОСЎ№әКчГзЈҝ
(3) Хюё®УліР°ьЙМөДәПН¬ТӘЗуЈ¬ФФЦІХвЕъКчГзөДіЙ»оВКұШРлІ»өНУЪ93%Ј¬·сФтіР°ьЙМіцЧКІ№ФФЈ»ИфіЙ»хВКҙпөҪ94%ТФЙП(ә¬94%)Ј¬ФтХюё®БнёшУи№ӨіМҝоЧЬ¶о6%өДҪұАшЈ¬ёГіР°ьЙМУҰИзәОСЎ№әКчГзІЕДЬ»сөГЧоҙуАыИуЈҝЧоҙуАыИуКЗ¶аЙЩЈҝ
Ўҫҙр°ёЎҝ(1)Ўўy=12x+20000(0ЈјxЎЬ3000)Ј»(2)Ўў№әВтјЧЦЦКчГзІ»ЙЩУЪ1800ҝГЗТІ»¶аУЪ3000ҝГЈ»(3)Ўў№әВтјЧЦЦКчГз1200ҝГЈ¬Т»ЦЦКчГз4800ҝГЈ¬ҝЙ»сөГЧоҙуАыИуЈ¬ЧоҙуАыИуКЗ50000ФӘ
ЎҫҪвОцЎҝ
КФМв·ЦОцЈә(1)ЎўёщҫЭАыИу=26НтЈӯЧЬіЙұҫөГіцәҜКэ№ШПөКҪЈ»(2)ЎўёщҫЭМвТвөГіцІ»өИКҪЈ¬И»әуЗуіцxөДИЎЦө·¶О§Ј»(3)ЎўўЩЎўөұіЙ»оВКІ»өНУЪ93%ЗТөНУЪ94%КұөГіцІ»өИКҪЧйЈ¬ЗуіцxөДИЎЦө·¶О§Ј¬И»әуёщҫЭәҜКэөДРФЦКЗуіцЧоЦөЈ¬ўЪөұіЙ»оВКөҪҙп94%ТФЙПБРіцІ»өИКҪЈ¬ЗуіцЧоҙуЦөЈ¬И»әуёщҫЭБҪХЯҪшРРСЎФс.
КФМвҪвОцЈә(1)ЎўyЈҪ260000Јӯ[20xЈ«32(6000Јӯx)Ј«8ЎБ6000]ЈҪ12xЈ«20000
ЧФұдБҝөДИЎЦө·¶О§КЗЈә0ЈјxЎЬ3000Ј»
(2)ЎўУЙМвТвЈ¬өГ12xЈ«20000ЎЭ260000ЎБ16%Ј¬ҪвөГЈәxЎЭ1800Ј¬ Ўа1800ЎЬxЎЬ3000Ј¬
№әВтјЧЦЦКчГзІ»ЙЩУЪ1800ҝГЗТІ»¶аУЪ3000ҝГЈ»
ЎўўЩИфіЙ»оВКІ»өНУЪ93%ЗТөНУЪ94%КұЈ¬УЙМвТвөГ
![]() ҪвөГ1200ЈјxЎЬ2400
ҪвөГ1200ЈјxЎЬ2400
ФЪyЈҪ12xЈ«20000ЦРЈ¬ ЎЯ12Јҫ0Ј¬ ЎаyЛжxөДФцҙу¶шФцҙуЈ¬
ЎаөұxЈҪ2400КұЈ¬yЧоҙуЈҪ48800Ј¬
ўЪИфіЙ»оВКҙпөҪ94%ТФЙП(ә¬94%)Ј¬Фт0.9xЈ«0.95(6000Јӯx)ЎЭ0.94ЎБ6000Ј¬ ҪвөГЈәxЎЬ1200Ј¬
УЙМвТвөГyЈҪ12xЈ«20000Ј«260000ЎБ6%ЈҪ12xЈ«35600Ј¬ ЎЯ12Јҫ0Ј¬ ЎаyЛжxөДФцҙу¶шФцҙуЈ¬
ЎаөұxЈҪ1200КұЈ¬yЧоҙуЦөЈҪ5000Ј¬
ЧЫЙПЛщКцЈ¬50000Јҫ48800
Ўа№әВтјЧЦЦКчГз1200ҝГЈ¬Т»ЦЦКчГз4800ҝГЈ¬ҝЙ»сөГЧоҙуАыИуЈ¬ЧоҙуАыИуКЗ50000ФӘЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіРЈіхТ»ЛщУРС§ЙъҪ«ФЪҙуАсМГДЪІОјУ2017ДкЎ°ФӘө©БӘ»¶Нн»бЎұЈ¬ИфГҝЕЕЧш30ИЛЈ¬ФтУР8ИЛОЮЧщО»Ј»ИфГҝЕЕЧш31ИЛЈ¬ФтҝХ26ёцЧщО»Ј¬ФтіхТ»Дкј¶№ІУР¶аЙЩГыС§ЙъЈҝЙиҙуАсМГДЪ№ІУРxЕЕЧщО»Ј¬ҝЙБР·ҪіМОӘ______________________
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎчABCЦРЈ¬DКЗBCұЯЙПөДТ»өгЈ¬EКЗADөДЦРөгЈ¬№эөгAЧчBCөДЖҪРРПЯҪ»CEөДСУіӨПЯУЪөгFЈ¬ЗТAFЈҪBDЈ¬Б¬ҪУBFЈ®
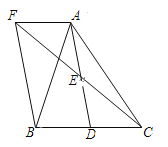
ЈЁ1Ј©ЗуЦӨDКЗBCөДЦРөгЈ»
ЈЁ2Ј©Из№ыABЈҪACЈ¬КФЕР¶ПЛДұЯРОAFBDКЗКІГҙЛДұЯРОЈ¬ІўЦӨГчДгөДҪбВЫЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
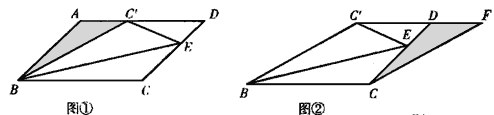
ЎҫМвДҝЎҝИзНјўЩЈ¬ЛДұЯРОABCDОӘЖҪРРЛДұЯРОЈ¬EФЪCDұЯЙПЈ¬Ҫ«ЎчBCEСШBE·ӯХЫЈ¬өгCёХәГВдФЪABұЯЙПөДөгCЎдҙҰ
ЈЁ1Ј©ФЪНјўЩЦРЈ¬ЗлЦұҪУРҙіцЛД¶ФПаөИөДПЯ¶ОЈ»
ЈЁ2Ј©Ҫ«НјўЩЦРөДЎчABCЎдјфПВІўЖҙҪУФЪНјўЪЦРЎчDCFөДО»ЦГЙПЈЁЖдЦРЎчABCЎдөДИэёц¶ҘөгAЎўBЎўCЎд·ЦұрУлЎчDCFөДИэёц¶ҘөгDЎўCЎўFЦШәПЈ¬ІўЗТНјўЪөДөгCЎдЎўDЎўFФЪН¬Т»ЦұПЯЙПЈ©КФЦӨГчНјўЪЦРөДЛДұЯРОBCFCЎдКЗБвРО.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝРҙіцТ»ёцФЪИэКУНјЦРё©КУНјУлЦчКУНјНкИ«ПаН¬өДјёәОМе Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИф№ШУЪxөД·ҪіМЈЁm©Ғ2Ј©x2+mx©Ғ1=0КЗТ»ФӘ¶юҙО·ҪіМЈ¬ФтmөДИЎЦө·¶О§КЗЈЁ Ј©
A.mЎЩ2
B.m=2
C.mЎЭ2
D.mЎЩ0
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘУӯҪУҪЁөіҫЕК®ЦЬДкЈ¬ДіЗшФЪёДЙЖ»·ҫіВМ»Ҝ·ҪГжЈ¬Ҫ«Н¶ИлЧКҪрУЙјЖ»®өДl 500 000ФӘМбёЯөҪ2 000 000ФӘЎЈЖдЦР2 000 000УГҝЖС§јЗКэ·ЁұнКҫОӘЈЁ Ј©
A. 0.2ЎБ107 B. 2ЎБ107 C. 2ЎБ106 D. 20ЎБ105
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com