【题目】五边形的外角和等于度．
科目：初中数学 来源： 题型：
【题目】我市为创建“国家级森林城市”，政府决定对江边一处废弃荒地进行绿化，要求栽植甲、乙两种不同的树苗共6000棵，且甲种树苗不得多于乙种树苗．某承包商以26万元的报价中标承包了这项工程．根据调查及相关资料表明：移栽一棵树苗的平均费用为8元，甲、乙两种树苗的购买价及成活率如表：
设购买甲种树苗x棵，承包商获得的利润为y元．请根据以上信息解答下列问题：
(1) 设y与x之间的函数关系式，并写出自变量x的取值范围；
(2) 承包商要获得不低于中标价16%的利润，应如何选购树苗？
(3) 政府与承包商的合同要求，栽植这批树苗的成活率必须不低于93%，否则承包商出资补栽；若成货率达到94%以上(含94%)，则政府另给予工程款总额6%的奖励，该承包商应如何选购树苗才能获得最大利润？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：点D是等腰直角三角形ABC斜边BC所在直线上一点（不与点B重合），连接AD．
（1）如图1，当点D在线段BC上时，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE．求证：BD=CE，BD⊥CE；
（2）如图2，当点D在线段BC延长线上时，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE．请画出图形。上述结论是否仍然成立，并说明理由；
（3）根据图2，请直接写出AD、BD、CD三条线段之间的数量关系。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“分组合作学习”成为我市推动课堂教学改革，打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本，对“分组合作学习”实施前后学生的学习兴趣变化情况进行调查分析，统计如下：
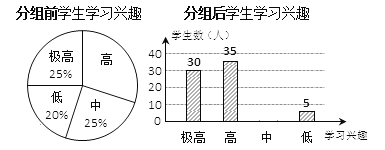
请结合图中信息解答下列问题：
（1）求出分组前学生学习兴趣为“高”的所占的百分比为_________；
（2）补全分组后学生学习兴趣的统计图；
（3）通过“分组合作学习”前后对比，请你估计全校2000名学生中学习兴趣获得提高的学生有多少人？请根据你的估计情况谈谈对“分组合作学习”这项举措的看法.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在平面直角坐标系中，△ABC是直角三角形,∠ACB=90,AC=BC,OA=1，OC=4，抛物线y=
+bx+c经过A，B两点，抛物线的顶点为D．
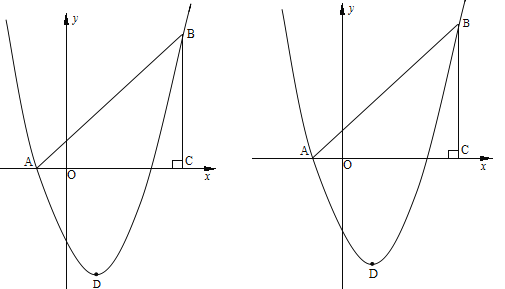
(1)、求b,c的值；
(2)、点E是直角三角形ABC斜边AB上一动点(点A、B除外)，过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；
(3)、在（2）的条件下：①求以点E、B、F、D为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形? 若存在，求出所有点P的坐标；若不存在，说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某儿童服装店欲购进A、B两种型号的儿童服装．经调查：B型号童装的进货单价是A型号童装的进货单价的两倍，购进A型号童装60件和B型号童装40件共用去2100元．
(1)、求A、B两种型号童装的进货单价各是多少元？
(2)、若该店每销售1件A型号童装可获利4元，每销售1件B型号童装可获利9元，该店准备用不超过6300元购进A、B两种型号童装共300件，且这两种型号童装全部售出后总获利不低于1795元．问该店应该怎样安排进货，才能使总获利最大？最大总获利为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现将三张形状、大小完全相同的平行四边形透明纸片分别放在方格纸中，方格纸中的每个小正方形的边长均为1，并且平行四边形 纸片的每个顶点与小正方形的顶点重合(如图①、图②、图③)．
图②矩形(正方形)
,
分别在图①、图②、图③中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，并把这两部分重新拼成符合下列要求的几何图形．
要求：
(1)在左边的平行四边形纸片中画一条裁剪线，然后在右边相对应的方格纸中，按实际大小画出所拼成的符合要求的几何图形．
(2)裁成的两部分在拼成几何图形时要互不重叠且不留空隙．
(3)所画出的几何图形的各顶点必须与小正方形的顶点重合．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
