
【题目】已知:点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合),连接AD.
(1)如图1,当点D在线段BC上时,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.求证:BD=CE,BD⊥CE;
(2)如图2,当点D在线段BC延长线上时,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.请画出图形。上述结论是否仍然成立,并说明理由;
(3)根据图2,请直接写出AD、BD、CD三条线段之间的数量关系。

【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、2AD2=BD2+CD2
【解析】
试题分析:(1)、首先根据等腰直角三角形的性质得出∠ABC=∠ACB=45°,然后根据同角的余角相等得出∠BAD=∠CAE,从而说明△BAD和△CAE全等,得出BD=CE,∠ACE=∠ABC=45°,然后根据∠BCE=∠ACB+∠ACE得出垂直;(2)、连接CE,然后根据(1)的同样证法得出答案;(3)、根据∠EAD=90°AE=AD得出ED=![]() AD,然后根据Rt△ECD的勾股定理得出答案.
AD,然后根据Rt△ECD的勾股定理得出答案.
试题解析:(1)、如图1,∵∠BAC=90°,AB=AC, ∴∠ABC=∠ACB=45°, ∵∠DAE=90°,
∴∠DAE=∠CAE+∠DAC=90°, ∵∠BAC=∠BAD+∠DAC=90°, ∴∠BAD=∠CAE,
在△BAD和△CAE中, 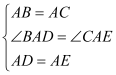 ∴△BAD≌△CAE(SAS), ∴BD=CE,∠ACE=∠ABC=45°.
∴△BAD≌△CAE(SAS), ∴BD=CE,∠ACE=∠ABC=45°.
∴∠BCE=∠ACB+∠ACE=90°, ∴BD⊥CE;
(2)、如图2,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.
与(1)同理可证CE=BD,CE⊥BD;
(3)、2AD2=BD2+CD2,
∵∠EAD=90°AE=AD, ∴ED=![]() AD, 在RT△ECD中,ED2=CE2+CD2, ∴2AD2=BD2+CD2
AD, 在RT△ECD中,ED2=CE2+CD2, ∴2AD2=BD2+CD2


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
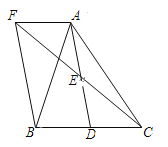
(1)求证D是BC的中点;
(2)如果AB=AC,试判断四边形AFBD是什么四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接建党九十周年,某区在改善环境绿化方面,将投入资金由计划的l 500 000元提高到2 000 000元。其中2 000 000用科学记数法表示为( )
A. 0.2×107 B. 2×107 C. 2×106 D. 20×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司10名员工某月份工资统计如下,则该公司10名职工这个月份工资的众数和中位数分别是( )
工资(元) | 2400 | 2600 | 2700 | 2900 |
人数(人) | 2 | 3 | 4 | 1 |
A. 2700元、2700元B. 2700元、2650元C. 2700元、2600元D. 2600元、2700元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com