
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
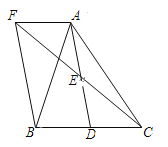
(1)求证D是BC的中点;
(2)如果AB=AC,试判断四边形AFBD是什么四边形,并证明你的结论.
【答案】(1)、证明过程见解析;(2)、矩形;证明过程见解析.
【解析】
试题分析:(1)、根据AF∥BD得出∠AFE=∠DCE,根据E是中点得出AE=DE,结合∠AEF=∠DEC得出△AEF和△EDC全等,从而得出DC=AF,根据AF=BD得出BD=DC,即中点;(2)、根据AF=BD以及AF∥BD得出四边形为平行四边形,根据AB=AC,D为BC的中点得出AD⊥BC,从而说明矩形.
试题解析:(1)、∵AF∥BD,∴∠AFE=∠DCE. ∵E是AD的中点,∴AE=DE.
又∵∠AEF=∠DEC,∴△AEF≌△DEC(AAS).∴DC=AF. 又∵AF=BD,∴BD=DC. ∴D是BC的中点
(2)、四边形AFBD是矩形.
∵AF=BD,AF∥BD, ∴四边形AFBD是平行四边形. ∵AB=AC,D是BC的中点,
∴AD⊥BC,∴∠ADB=90°. ∴四边形AFBD是矩形.


科目:初中数学 来源: 题型:
【题目】
①1是绝对值最小的数;
②0既不是正数,也不是负数;
③一个有理数不是整数就是分数;
④0的绝对值是0.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=acm,AB=bcm(a>b>4),半径为2cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).
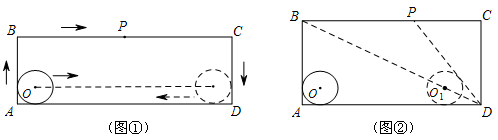
(1)如图①,点P从A→B→C→D,全程共移动了 cm(用含a、b的代数式表示);
(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离;
(3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
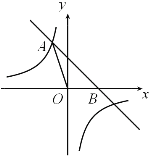
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.
(1)求该反比例函数的表达式;
(2)若P为y轴上的点,且△AOP的面积是△AOB的面积的![]() ,请求出点P的坐标.
,请求出点P的坐标.
(3)写出直线![]() 向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标。
向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快推进教育现代化,某中学计划分批购买部分A品牌电脑和B品牌课桌.下表是前两次购买的情况:
A品牌电脑的数量 (单位:台) | B品牌课桌的数量 (单位:张) | 总价 (单位:元) | |
第一次 | 10 | 200 | 70000 |
第二次 | 15 | 100 | 75000 |
(1)每台A品牌电脑和每张B品牌课桌的价格各是多少元?
(2)在“五·一”黄金周期间,经销商对一次性购买量大的客户打折优惠:一次性购买A品牌电脑不少于50台,按9折优惠;一次性购买B品牌课桌不少于450张,按8折优惠.如果学校再次购买A品牌电脑和B品牌课桌若干,恰好花去24万元,并且均享受了优惠,那么学校可能有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市为创建“国家级森林城市”,政府决定对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗.某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价及成活率如表:

设购买甲种树苗x棵,承包商获得的利润为y元.请根据以上信息解答下列问题:
(1) 设y与x之间的函数关系式,并写出自变量x的取值范围;
(2) 承包商要获得不低于中标价16%的利润,应如何选购树苗?
(3) 政府与承包商的合同要求,栽植这批树苗的成活率必须不低于93%,否则承包商出资补栽;若成货率达到94%以上(含94%),则政府另给予工程款总额6%的奖励,该承包商应如何选购树苗才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合),连接AD.
(1)如图1,当点D在线段BC上时,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.求证:BD=CE,BD⊥CE;
(2)如图2,当点D在线段BC延长线上时,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.请画出图形。上述结论是否仍然成立,并说明理由;
(3)根据图2,请直接写出AD、BD、CD三条线段之间的数量关系。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com