
【题目】已知:在矩形ABCD中,AB=8,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2. 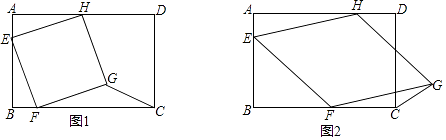
(1)如图1,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图2,当四边形EFGH为菱形时,设BF=x,△GFC的面积为S,求S关于x的函数关系式,并写出函数的定义域.
【答案】
(1)解:如图1,过点G作GM⊥BC,垂足为M.
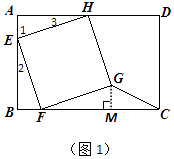
由矩形ABCD可知:∠A=∠B=90°,
由正方形EFGH可知:
∠HEF=90°,EH=EF,
∴∠1+∠2=90°,
又∠1+∠3=90°,
∴∠3=∠2,
∴△AEH≌△BFE.
∴BF=AE=2,
同理可证:△MGF≌△BFE,
∴△MGF≌△AEH,
∴GM=AE=2,
又 FC=BC﹣BF=12﹣2=10,
∴S△GFC= ![]() FCGM=
FCGM= ![]() ×10×2=10.
×10×2=10.
(2)解:如图2,过点G作GM⊥BC,垂足为M,连接HF.

由矩形ABCD得:AD∥BC,
∴∠AHF=∠HFM,
由菱形EFGH得:EH∥FG,EH=FG,
∴∠1=∠2,
∴∠3=∠4,
又∠A=∠M=90°,EH=FG,
∴△MGF≌△AEH,
∴GM=AE=2,
又 BF=x,∴FC=12﹣x,
∴S△GFC= ![]() FCGM=
FCGM= ![]() (12﹣x)2=12﹣x,
(12﹣x)2=12﹣x,
即:S=12﹣x,
定义域: ![]() .
.
【解析】(1)只要证明△AEH≌△BFE.推出BF=AE=2,由△MGF≌△BFE,推出△MGF≌△AEH,求出FC、GM即可解决问题.(2)如图2,过点G作GM⊥BC,垂足为M,连接HF,根据S△GFC= ![]() FCGM,计算即可.
FCGM,计算即可.
【考点精析】本题主要考查了菱形的性质和矩形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】温度通常有两种表示方法:华氏度(单位:℉)与摄氏度(单位:℃),已知华氏度数y与摄氏度数x之间是一次函数关系,如表列出了部分华氏度与摄氏度之间的对应关系:
摄氏度数x(℃) | … | 0 | … | 35 | … | 100 | … |
华氏度数y(℉) | … | 32 | … | 95 | … | 212 | … |
(1)选用表格中给出的数据,求y关于x的函数解析式(不需要写出该函数的定义域);
(2)已知某天的最低气温是﹣5℃,求与之对应的华氏度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( ) 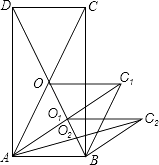
A.![]() cm2
cm2
B.![]() cm2
cm2
C.![]() cm2
cm2
D.![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程kx2+(k+2)x+ ![]() =0有两个不相等的实数根;
=0有两个不相等的实数根;
(1)求k的取值范围;
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表:
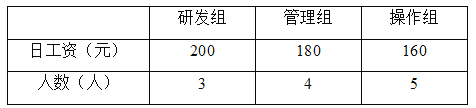
现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中正确的有( )
①平均日工资增大 ②日工资的方差减小
③日工资的中位数不变 ④日工资的众数不变
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com