
【题目】如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( ) 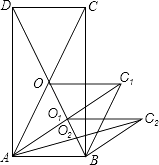
A.![]() cm2
cm2
B.![]() cm2
cm2
C.![]() cm2
cm2
D.![]() cm2
cm2
【答案】B
【解析】方法一: 解:设矩形ABCD的面积为S=20cm2 ,
∵O为矩形ABCD的对角线的交点,
∴平行四边形AOC1B底边AB上的高等于BC的 ![]() ,
,
∴平行四边形AOC1B的面积= ![]() S,
S,
∵平行四边形AOC1B的对角线交于点O1 ,
∴平行四边形AO1C2B的边AB上的高等于平行四边形AOC1B底边AB上的高的 ![]() ,
,
∴平行四边形AO1C2B的面积= ![]() ×
× ![]() S=
S= ![]() ,
,
…,
依此类推,平行四边形AO4C5B的面积= ![]() =
= ![]() =
= ![]() (cm2).
(cm2).
故选:B.
方法二: q=
q= ![]() ,a1=10,
,a1=10,
∴an=10 ![]() ,∴a5=10
,∴a5=10 ![]() =
= ![]() .
.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】“4000辆自行车、187个服务网点”,台州市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机构对2016年微信用户的职业颁布进行了随机抽样调查(职业说明:A:党政机关、军队,B:事业单位,C:企业,D:自由职业及人体户,E:学生,F:其他),图1和图2是根据调查数据绘制而成的不完整的统计图.请根据图中提供的信息,解答下列问题:
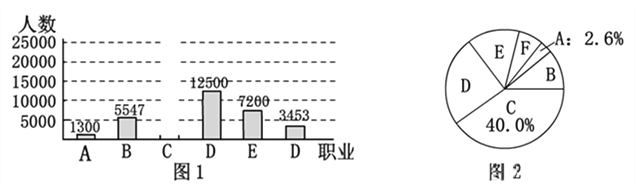
(1)该机构共抽查微信用户___________人;
(2)在图.1中,补全条形统计图;
(3)在图2中,“D”用户所对应扇形的圆心角度数为___________度;
(4)2016年微信用户约有7.5亿人,估计“E”用户大约有________亿人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形ABCD中,AB=8,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2. 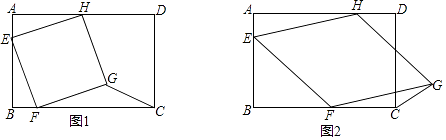
(1)如图1,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图2,当四边形EFGH为菱形时,设BF=x,△GFC的面积为S,求S关于x的函数关系式,并写出函数的定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果![]()
![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,![]()
![]() )=_______.
)=_______.
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com