练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．关于x的一元二次方程x2-2x+m=0有两个不相等的实数根．请你写出一个满足条件的m值：m=0．

    分析 若一元二次方程有两不等根，则根的判别式△=b2-4ac＞0，建立关于m的不等式，求出m的取值范围．

    解答 解：∵方程有两个不相等的实数根，a=1，b=-2，c=m，
    ∴△=b2-4ac=（-2）2-4×1×m＞0，
    解得m＜1，
    故答案是：0．

    点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．若关于x的不等式组$\left\{\begin{array}{l}{x＞m}\\{x＜8}\end{array}\right.$无解，则m的取值范围是m≥8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解方程组
    （1）$\left\{\begin{array}{l}{x-2y=z}\\{3x+2y=1}\\{2x-y=z+\frac{1}{2}}\end{array}\right.$；
    （2）$\left\{\begin{array}{l}{3x+2y+5z=2}\\{x-2y-z=6}\\{4x+2y-7z=30}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

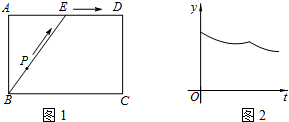
    14．为了锻炼学生身体素质，训练定向越野技能，某校在一公园内举行定向越野挑战赛．路线图如图1所示，点E为矩形ABCD边AD的中点，在矩形ABCD的四个顶点处都有定位仪，可监测运动员的越野进程，其中一位运动员P从点B出发，沿着B-E-D的路线匀速行进，到达点D．设运动员P的运动时间为t，到监测点的距离为y．现有y与t的函数关系的图象大致如图2所示，则这一信息的来源是（　　）
    A．监测点AB．监测点BC．监测点CD．监测点D

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．实数a，b，c，d在数轴上的对应点的位置如图所示，其中互为相反数的两个数是（　　）
    A．a和dB．a和cC．b和dD．b和c

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

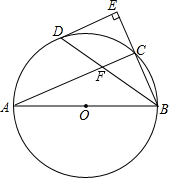    11．如图，已知AB为⊙O的直径，C为⊙O上异于A、B的一个动点，作∠ABC的平分线交⊙O于点D，过点D作⊙O的切线与BC的延长线交于点E，连接BD交AC于点F，小明经操作发现如下2个结论：①∠E为直角；②FA=FB，请你分别判断这两个结论是否成立？若成立，请给予证明；若不成立，请补充条件，使之成立．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．据北京市商务委表示，除夕至初五，21家节能减排补贴商品定点销售企业销售额超过28000000元．将28000000用科学记数法表示应为（　　）
    A．0.28×108B．2.8×108C．2.8×107D．28×106

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

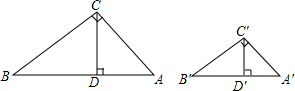    10．如图，在Rt△ABC和Rt△A′B′C′中，∠ACB=∠A′B′C′中，∠ACB=∠A′C′B′=90°，CD，C′D′分别是两个三角形斜边上的高，且CD：C′D′=AC：A′C′．证明：△ABC∽△A′B′C′．
    思路探究：
    （1）要证明△ABC∽△A′B′C′，需要证明∠A=∠A′．
    （2）要证明（1）中的条件，需证明△ADC∽△A′D′C′．
    证明：

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知点P1，P2在反比例函数y=$\frac{4}{x}$（x＞0）的图象上，△P1OA1，△P2A1A2是等腰直角三角形，斜边OA1，A1A2都在x轴上，根据上述条件，你能求得点A2的坐标吗？

    查看答案和解析>>

    同步练习册答案