Question

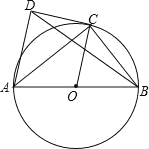
【题目】如图，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．

（1）求证：AC平分∠DAB；

（2）若sin∠ABC=，求tan∠BDC的值．

Answer 1

【答案】（1）证明见解析；

（2）tan∠CDB=tan∠DBM===.

【解析】

试题分析：（1）先证明AD∥OC，得∠DAC=∠ACO，再根据OA=OC得∠OAC=∠OCA，由此即可证明．

（2）连接BM、OC交于点N，根据sin∠ABC=sin∠BCN==，设BN=4k，BC=5k，则CN=3k，求出DM，BM，根据tan∠CDB=tan∠DBM=即可解决问题．

试题解析：（1）∵DC是⊙O切线，

∴OC⊥CD，∵AD⊥CD，

∴AD∥CO，

∴∠DAC=∠ACO，

∵OA=OC，

∴∠OAC=∠ACO，

∴∠DAC=∠CAO，

∴AC平分∠DAB．

（2）连接BM、OC交于点N．

∵AB是直径，

∴∠AMB=90°，∵AD∥OC，

∴∠ONB=∠AMB=90°=∠CNB，

∵OC=OB，

∴∠OCB=∠OBC，

∴sin∠ABC=sin∠BCN==，设BN=4k，BC=5k，则CN=3k，

∵∠CDM=∠DMN=∠DCN=90°，

∴四边形DMNC是矩形，

∴DM=CN=3k，MN=BN=4k，CD∥BM，

∴∠CDB=∠DBM，

∴tan∠CDB=tan∠DBM===．